F3-Fadenpendel
Die einfachste Beschreibung eines Pendels geht von einer in einem
Punkt konzentrierten Masse 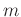 aus, die durch einen als masselos
angenommenen Faden mit der Länge
aus, die durch einen als masselos
angenommenen Faden mit der Länge 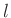 im Schwerefeld fixiert ist. Wird
der Massepunkt aus der Ruhelage um den Winkel
im Schwerefeld fixiert ist. Wird
der Massepunkt aus der Ruhelage um den Winkel 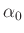 ausgelenkt und
wirken danach außer der Schwerkraft keine weiteren Kräfte auf den
Massepunkt ein, so führt er eine periodische Bewegung um die Ruhelage
aus. Die Bewegungsgleichung für ein solches ungedämpftes
mathematisches Pendel lautet:
ausgelenkt und
wirken danach außer der Schwerkraft keine weiteren Kräfte auf den
Massepunkt ein, so führt er eine periodische Bewegung um die Ruhelage
aus. Die Bewegungsgleichung für ein solches ungedämpftes
mathematisches Pendel lautet:
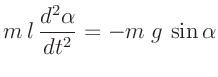 |
(1) |
Mit der Beschränkung auf unendlich kleine Winkel kann diese durch die
Näherung
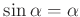 in die Schwingungsgleichung eines
ungedämpften harmonischen Oszillators überführt werden.
in die Schwingungsgleichung eines
ungedämpften harmonischen Oszillators überführt werden.
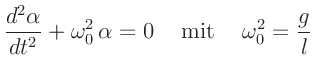 |
(2) |
Aus deren Lösung ergibt sich für die Periodendauer des mathematischen
Pendels:
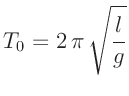 |
(3) |
Ohne die Beschränkung auf unendlich kleine Winkel erfordert die Lösung
der Gleichung1 einen wesentlich höheren
mathematischen Aufwand. Das sich ergebende vollständige elliptische
Integral erster Art kann durch eine Reihenentwicklung gelöst
werden und führt auf:
Die vollständige Herleitung findet man zum Beispiel in
R.M.Dreizler, C.S.Lüdde (2008) (Kapitel 4.2.1, Seiten 162-169).
Bei einer Beschränkung auf hinreichend kleine Winkel (einige Grad)
kann diese Gleichung nach dem ersten Winkelterm abgebrochen werden und
ergibt mit der Kleinwinkelnäherung
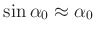 den in
fast allen Fällen ausreichenden Ausdruck für die Periodendauer eines
mathematischen Pendels
den in
fast allen Fällen ausreichenden Ausdruck für die Periodendauer eines
mathematischen Pendels
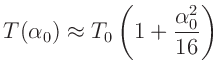 |
(4) |
Erst wenn der Fehler, der durch den Abbruch der Reihenentwicklung und
die erfolgte Kleinwinkelnäherung entsteht, die Größenordnung der
Messunsicherheit erreicht, kann die Näherung (Gleichung4)
nicht mehr angewendet werden.
Ein mathematisches Pendel lässt sich für praktische Messungen nicht
realisieren. Der verwendete Massekörper besitzt immer eine endliche
Ausdehnung und damit ein eigenes Trägheitsmoment um seinen
Schwerpunkt, das die Periodendauer beeinflusst.
Für einen im Abstand 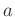 zu seinem Schwerpunkt aufgehängten starren
Körper mit dem auf die Schwingungsachse bezogenem Trägheitsmoment
zu seinem Schwerpunkt aufgehängten starren
Körper mit dem auf die Schwingungsachse bezogenem Trägheitsmoment 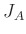 lautet die Bewegungsgleichung
lautet die Bewegungsgleichung
aus der sich analog zum mathematischen Pendel die Lösung für unendlich
kleine Amplituden zu
ergibt. Aus dem Vergleich mit der Periodendauer des mathematischen
Pendels (Gleichung3) und der Anwendung des Steinerschen
Satzes folgt, dass für die Länge 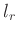 eines mathematischen Pendels
gleicher Periodendauer gelten muss:
eines mathematischen Pendels
gleicher Periodendauer gelten muss:
wobei 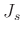 das auf den Schwerpunkt bezogene Trägheitsmoment des
physikalischen Pendels ist. Der Term
das auf den Schwerpunkt bezogene Trägheitsmoment des
physikalischen Pendels ist. Der Term 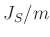 wird im weiteren mit
wird im weiteren mit 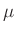 bezeichnet. Die so definierte reduzierte Pendellänge
bezeichnet. Die so definierte reduzierte Pendellänge
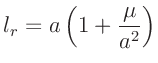 |
(5) |
führt das physikalische Pendel auf ein mathematisches Pendel zurück.
Das Fadenpendel kann als ein Spezialfall des physikalischen Pendels
betrachtet werden. Die gesamte Masse ist in dem an einem dünnen Faden,
meist ein Stahldraht, aufgehängten, homogenen Pendelkörper
konzentriert. Die Masse des Fadens wird gegenüber der Masse des
Pendelkörpers vernachlässigt. Damit wird 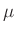 nur durch die Form des
Pendelkörpers bestimmt und kann berechnet werden. So gilt für eine
Kugel mit dem Radius
nur durch die Form des
Pendelkörpers bestimmt und kann berechnet werden. So gilt für eine
Kugel mit dem Radius 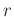
und für einen Zylinder mit dem Durchmesser 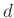 und der Höhe
und der Höhe 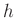 , dessen
Querachse parallel zur Schwingungsachse orientiert ist:
, dessen
Querachse parallel zur Schwingungsachse orientiert ist:
Die Gleichung5 für die reduzierte Pendellänge kann dann zur
Korrektur der gemessen Länge des Fadenpendels 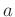 benutzt werden. Für
genauere Messungen ist diese Näherung allerdings nicht mehr
ausreichend. Das Trägheitsmoment des Fadens muss mitberücksichtigt werden
1.
benutzt werden. Für
genauere Messungen ist diese Näherung allerdings nicht mehr
ausreichend. Das Trägheitsmoment des Fadens muss mitberücksichtigt werden
1.
Zur Bestimmung der Erdbeschleunigung 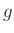 mit einem Fadenpendel sollte
nach den obigen Überlegungen die Messung der Periodendauer
mit einem Fadenpendel sollte
nach den obigen Überlegungen die Messung der Periodendauer
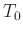 für einen vorgegebenen Schwerpunktabstand
für einen vorgegebenen Schwerpunktabstand 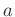 ausreichen. Dabei sind die Gleichungen4 zur Korrektur der
Amplitudenabhängigkeit und5 zur Korrektur der Pendellänge
entsprechend anzuwenden. Zu Anfang des 19.Jahrhunderts wurde diese
Methode
ausreichen. Dabei sind die Gleichungen4 zur Korrektur der
Amplitudenabhängigkeit und5 zur Korrektur der Pendellänge
entsprechend anzuwenden. Zu Anfang des 19.Jahrhunderts wurde diese
Methode
Im Jahr 1828 hat F.W.Bessel (1828) in seiner Schrift
,,Untersuchungen über die Länge des einfachen
Secundenpendels`` einen anderen Weg zur Bestimmung der
Erdbeschleunigung beschrieben. Er benutzte dazu ein Fadenpendel dessen
Länge er um einen genau bekannten Betrag 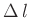 verändern
konnte. Aus den beiden Periodendauern des kurzen und des langen
Pendels und dem bekannten Längenunterschied lässt sich
verändern
konnte. Aus den beiden Periodendauern des kurzen und des langen
Pendels und dem bekannten Längenunterschied lässt sich 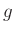 berechnen
berechnen
wobei 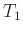 und
und 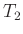 die auf eine unendlich kleine Amplitude
korrigierten Messwerte für das lange beziehungsweise das kurze Pendel
sind.
die auf eine unendlich kleine Amplitude
korrigierten Messwerte für das lange beziehungsweise das kurze Pendel
sind.
Wird das Pendel in mehreren Stufen
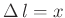 verkürzt und
der Zusammenhang
verkürzt und
der Zusammenhang
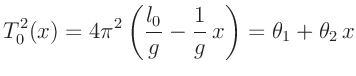 |
(6) |
ausgewertet, so kann aus dem Anstieg 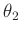 der sich ergebenden
Geraden der Wert von
der sich ergebenden
Geraden der Wert von 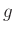 berechnet werden. Dabei bleibt jedoch die
sich ergebende, nichtlineare Veränderung von
berechnet werden. Dabei bleibt jedoch die
sich ergebende, nichtlineare Veränderung von 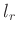 (Gleichung5) unberücksichtigt. Die notwendige
Amplitudenkorrektur (Gleichung4) erfordert die ungefähre
Kenntnis des unbekannten Wertes von
(Gleichung5) unberücksichtigt. Die notwendige
Amplitudenkorrektur (Gleichung4) erfordert die ungefähre
Kenntnis des unbekannten Wertes von 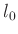 .
.
Diese Schwierigkeiten treten nicht auf, wenn man den vollständigen,
nichtlinearen Zusammenhang zwischen der gemessenen Zeit 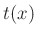 für
für 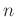 Schwingungsperioden zur Auswertung benutzt.
Schwingungsperioden zur Auswertung benutzt.
In dieser Funktion ist sowohl die Amplitudenkorrektur als auch die
Berücksichtigung der reduzierten Pendellänge enthalten, während vom
Einfluss des Fadens und dessen unterschiedlicher Länge abstrahiert
wird.
Verglichen mit dem Fadenpendel ist eine wesentlich genauere Bestimmung
der Erdbeschleunigung mit Hilfe des erstmals von Bohnenberger 1811
vorgeschlagenen Reversionspendel (Versuch M9) möglich.
Auswertung mit extern generierter Datentabelle
Der erste Schritt zur Auswertung ist die Erstellung einer
Datentabelle, die die im weiteren benötigten von 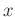 abhängigen
Messwerte
abhängigen
Messwerte 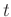 und deren Unsicherheit
und deren Unsicherheit 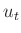 sowie die daraus
berechneten Größen
sowie die daraus
berechneten Größen
enthält. Als Längeneinheit bietet sich in diesem Versuch Millimeter und als
Zeiteinheit Sekunden an.
Tabelle 1:
Beispiel einer Datentabelle, erstellt mit einer Tabellenkalkulation.
Die erste Zeile ist mit # als Kommentar gekennzeichnet
| #x |
tmeasure |
utmeasure |
T0 |
uT0 |
T0quadrat |
uTOquadrat |
| 0. |
41.45 |
0.039480 |
2.071668 |
0.001973 |
4.291809 |
0.008176 |
| 0. |
41.37 |
0.039479 |
2.067670 |
0.001973 |
4.275258 |
0.00816 |
| 40. |
40.74 |
0.039472 |
2.036116 |
0.001973 |
4.145769 |
0.008033 |
| 40. |
40.75 |
0.039472 |
2.036616 |
0.001973 |
4.147805 |
0.008035 |
| 80. |
39.97 |
0.039463 |
1.997560 |
0.001972 |
3.990245 |
0.007879 |
| 80. |
39.96 |
0.039463 |
1.997060 |
0.001972 |
3.988249 |
0.007877 |
| 120. |
39.13 |
0.039453 |
1.955499 |
0.001972 |
3.823975 |
0.007711 |
| 120. |
39.16 |
0.039453 |
1.956998 |
0.001972 |
3.829841 |
0.007717 |
| 160. |
38.31 |
0.039443 |
1.914429 |
0.001971 |
3.665040 |
0.007547 |
| 160. |
38.35 |
0.039444 |
1.916428 |
0.001971 |
3.672697 |
0.007555 |
| 200. |
37.48 |
0.039434 |
1.872851 |
0.001970 |
3.507573 |
0.007381 |
| 200. |
37.52 |
0.039434 |
1.874850 |
0.001971 |
3.515063 |
0.007389 |
| 240. |
36.59 |
0.039423 |
1.828265 |
0.001970 |
3.342553 |
0.007203 |
| 240. |
36.65 |
0.039424 |
1.831263 |
0.001970 |
3.353524 |
0.007215 |
| 280. |
35.69 |
0.039413 |
1.783167 |
0.001969 |
3.179684 |
0.007023 |
| 280. |
35.65 |
0.039413 |
1.781168 |
0.001969 |
3.172560 |
0.007015 |
| 320. |
34.70 |
0.039402 |
1.733558 |
0.001968 |
3.005222 |
0.006825 |
| 320. |
34.80 |
0.039403 |
1.738553 |
0.001969 |
3.022568 |
0.006845 |
| 360. |
33.85 |
0.039392 |
1.690925 |
0.001968 |
2.859226 |
0.006655 |
| 360. |
33.83 |
0.039392 |
1.689926 |
0.001968 |
2.855848 |
0.006651 |
| 400. |
32.87 |
0.039380 |
1.641776 |
0.001967 |
2.695428 |
0.006459 |
| 400. |
32.86 |
0.039380 |
1.641276 |
0.001967 |
2.693788 |
0.006457 |
|
Diese Tabelle sollte unter einem eindeutigen Namen
(z.B. ¨daten-F3.txt¨) im Arbeitsverzeichnis von
GnuPlot abgelegt werden. Danach kann das Programm
GnuPlot
gestartet werden. Als erstes sollte der Namen der Datendatei als
Wert einer Variable festgelegt werden,
datafile="data-F3.txt"
damit bei späteren Änderungen des Dateinamens dieser nur einmal und
nicht bei jedem Vorkommen geändert werden muss.
Damit später die erste Zeile als Kommentarzeile erkannt
wird, ist das Kommentarzeichen für Datendateien festzulegen.
set datafile commentschars #"
Dies entspricht der Vorgabeeinstellung auf den meisten
Betriebssystemen. Es können auch mehrere verschiedene Zeichen
festgelegt werden, zum Beispiel:
set datafile commentschars #%!"
Alle Zeilen die mit einem dieser Zeichen beginnen werden beim Lesen der
Datendatei ignoriert. Im obigen Beispiel wird die erste Zeile mit den
Spaltenbezeichnungen übersprungen.
Als nächstes erfolgt die Definition der Fitfunktion für das lineare
Modell (Gleichung6)
tlin(x) = a1 + a2 * x
Da GnuPlot für aller Fitmodelle den gleichen iterativen
Algorithmus verwendet müssen auch für in den Parametern lineare
Probleme Startwerte vorab definiert werden. Diese lassen sich einfach
mit Hilfe der Messdaten durch Abschätzung des Anfangs- und Endpunktes
der vermuteten Geraden festlegen.
a1 = 4.2
a2 =(2.7 -4.2)/400
Im nächsten Schritt sind einige Einstellungen für die Ausgabe der
Ergebnisse der Fit-Prozedur vorzunehmen.
- Bei der Berechnung der Unsicherheiten der
Parameter soll der Wert von 'reduced chisquare` als
Varianz der Gewichtseinheit berücksichtigt werden.
- Die berechneten Unsicherheiten der Parameter sollen in eigenen
Variablen mit dem Namen der Parameter ergänzt um ¨_err¨
abgespeichert werden.
- Die berechneten Kovarianzterme sollen in eigenen Variablen
gespeichert werden, die mit FIT_COV_ beginnen, gefolgt von den
beiden durch einen ¨_¨ getrennten Parameternamen.
set fit errorscaling
set fit errorvariables
set fit covariancevariables
show fit
Danach werden alle Einstellungen der Prozedur fit zusammengefasst
ausgegeben. Als nächstes kann sie aufgerufen werden. Es werden die
Spalte 1 (x-Werte) und die Spalte 6 (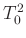 ) als Datenpunkte sowie
die Spalte 7 (
) als Datenpunkte sowie
die Spalte 7 (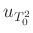 ) für die Berechnung der Gewichte benutzt.
) für die Berechnung der Gewichte benutzt.
fit tlin(x) datafile using 1:6:7 yerr via a1,a2
Im Terminalfenster werden eine Vielzahl an Informationen über den
Verlauf und das Ergebnis des Fits ausgegeben, die zusätzlich auch in
der Datei ¨fit.log¨ festgehalten werden.
Die wichtigsten Ergebnisse, die in extra Variablen gespeicherten
Werte, können auch noch einmal zusätzlich mit der vollen
Rechengenauigkeit ausgegeben werden.
print "a1 = ",a1
print "a2 = ",a2
print "sigma[a1] = ",a1_err
print "sigma[a2] = ",a2_err
print "COV[a1,a2] = ",FIT_COV_a1_a2
Die gesuchten Werte von 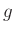 und
und 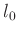 sowie deren Unsicherheiten
lassen sich daraus berechnen und ausgeben.
sowie deren Unsicherheiten
lassen sich daraus berechnen und ausgeben.
print "g = ", -4*pi**2/a2
print "ug = ", 4*pi**2/a2**2*a2_err
print "l0 = ", -a1/a2
print "ul0 = ",-1/a2*sqrt(a1_err**2-2*a1/a2*FIT_COV_a1_a2+(a1/a2*a2_err)**2)
Mit den oben angegebene Daten erhält man aus dem linearen Fit
-
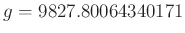 und
und
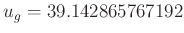 in
in 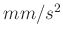
-
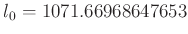 und
und
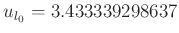 in
in 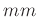
Gerundet nach DIN 1333 ergibt das
-
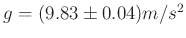
-
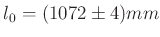
als Endergebnis.
Abbildung 1:
Abhängigkeit des Quadrates der Periodendauer von der Verkürzung x
![\begin{figure}\begin{center}
\begin{picture}(114,76)
%% 114 x 76 mm
\include...
...width=114mm]{Abbildungen/T0quadrat-x}
\end{picture}
\end{center}\end{figure}](Timg86.png) |
Für die graphische Darstellung der Datenpunkte mit Fehlerbalken
zusammen mit der angepassten Gerade sind die Achsenbeschriftungen und der
Wertebereich der Achsen festzulegen bevor die plot Prozedur aufgerufen wird.
set xlabel "x [mm]"
set ylabel "T_0^2 [s^2]"
set xrange [-10:410]
set yrange [2.5:4.5]
plot datafile using 1:6:7 with errorbars pt 7 ps 0.25 title "measured data",\
tlin(x) title "linear fit"
Ändert man vor dem plot Befehl das Ausgabe Terminal für die erzeugte
Grafik, wird diese in dem gewählten Ausgabeformat in einer Datei
abgelegt, die später in andere Dokumente eingebunden werden kann. Mit
den Befehlen
set terminal pdf linewidth 1 size 4.5,3
set output "T0quadrat-x.pdf"
schreibt die plot-Prozedur ein 114x76mm (4,5x3inch) großes
PDF-Dokument, das die vollständige Grafik mit allen Beschriftungen
enthält, in die Datei mit dem als Ausgabeziel angegebenen Namen.
Anstelle des linearen Geradenausgleichs kann auch direkt der
Zusammenhang zwischen der gemessenen Zeit 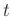 für
für 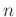 Perioden und der
Verkürzung des Pendelfadens
Perioden und der
Verkürzung des Pendelfadens 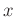 (Gleichung7) für einen
nichtlinearen Fit genutzt werden. Die Einstellungen für die
Fit-Prozedur, die festlegen, in welcher Art und Weise die Ausgabe der
Ergebnisse erfolgt, sind die gleichen wie für den linearen Fit. Die zu
bestimmenden Parameter sind
(Gleichung7) für einen
nichtlinearen Fit genutzt werden. Die Einstellungen für die
Fit-Prozedur, die festlegen, in welcher Art und Weise die Ausgabe der
Ergebnisse erfolgt, sind die gleichen wie für den linearen Fit. Die zu
bestimmenden Parameter sind
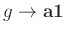 und
und
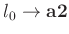 . Auf den ersten Blick könnte man
auch den Wert von
. Auf den ersten Blick könnte man
auch den Wert von
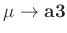 als möglichen
Fitparameter ansehen. Auf Grund der sich dann ergebenden sehr starken
Korrelationen zwischen diesen drei Parametern führt ein solcher Fit
nicht zu sinnvollen Ergebnissen. Damit kann die in den zwei gewählten
Parametern nichtlineare Modellfunktion
als möglichen
Fitparameter ansehen. Auf Grund der sich dann ergebenden sehr starken
Korrelationen zwischen diesen drei Parametern führt ein solcher Fit
nicht zu sinnvollen Ergebnissen. Damit kann die in den zwei gewählten
Parametern nichtlineare Modellfunktion
tnl(x) = 2*n*pi*(1+1/16*(a/(a1-x))**2)*sqrt((a1-x)/a2*(1+mu/(a1-x)**2))
definiert werden. Um diese Funktion anzuwenden, sind die Variablen für
die Anzahl der gemessenen Schwingungsperioden n und die benutzte
Auslenkung des Pendels a mit den im Experiment verwendeten Werten zu
belegen. Desweiteren wird für die Variable mu der Wert von
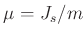 des zylindrischen Pendelkörpers benötigt, der aus den
gemessenen Werten des Durchmessers und der Höhe berechnet wurde. Als
Startwerte für a1 und a2 können plausible Werte von
des zylindrischen Pendelkörpers benötigt, der aus den
gemessenen Werten des Durchmessers und der Höhe berechnet wurde. Als
Startwerte für a1 und a2 können plausible Werte von
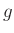 und der gemessene Schwerpunktabstand bei maximaler Pendellänge
genutzt werden, oder man verwendet die aus dem linearen Fit
berechneten Werte.
und der gemessene Schwerpunktabstand bei maximaler Pendellänge
genutzt werden, oder man verwendet die aus dem linearen Fit
berechneten Werte.
n=20
a=85
mu=320
a1=l0
a2=g
Die Messunsicherheiten aller gemessenen Zeiten sind nahezu gleich, da
die durch das Starten und Stoppen der Uhr per Hand bedingte
Standardabweichung der Zeitmessung nicht oder nur sehr geringfügig von
der gemessenen Zeit abhängt. Der systematische Restfehler der
verwendeten Stoppuhr ist in dem gegebenen Zeitintervall ebenfalls
nahezu unabhängig vom Messwert. Aus diesem Grund kann hier auf eine
Gewichtung mit dem Fehler der Zeitmessung verzichtet werden. Die
resultierende Gewichtsmatrix wäre die Einheitsmatrix.
Da die eingestellten Wertebereiche für die graphische Darstellung auch
die Wertebereiche für die im Fit verwendeten Datenpunkte festlegen,
sind diese Definitionen wieder aufzuheben.
unset xrange
unset yrange
Danach wird die Fit-Prozedur mit
fit tnl(x) datafile using 1:2 via a1,a2
gestartet. Die Ergebnisse für die gefundenen
Fitparameter, die auch im Terminalfenster angezeigt werden, können
zusätzlich noch mit der vollen Rechengenauigkeit ausgegeben werden.
print "a1 = ",a1
print "a2 = ",a2
print "sigma[a1] = ",a1_err
print "sigma[a2] = ",a2_err
Damit lautet das Ergebnis der nichtlinearen Fits
-
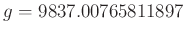 und
und
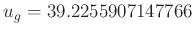 in
in 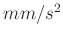
-
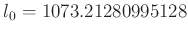 und
und
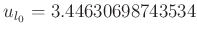 in
in 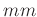
Gerundet nach DIN 1333 ergibt das
-
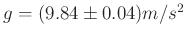
-
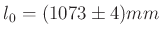
als Endergebnis, welches sich im Rahmen der Unsicherheit nicht von dem
Ergebnis des linearen Fits unterscheidet. Der Zusammenhang zwischen
Abbildung 2:
Abhängigkeit der gemessenen Zeit (20 Perioden) von der Verkürzung x
![\begin{figure}\begin{center}
\begin{picture}(114,76)
%% 114 x 76 mm
\includegraphics[width=114mm]{Abbildungen/t-x}
\end{picture}
\end{center}\end{figure}](Timg103.png) |
der gemessenen Zeit und der Verkürzung des Pendels kann in einer
Grafik dargestellt werden. Vor dem Aufruf der Plot-Prozedur sind die
Wertebereiche der Achsen und deren Beschriftungen festzulegen.
set xrange [-10:410]
set yrange [32:42]
set xlabel "x [mm]
set ylabel t [s]
plot datafile using 1:2:3 with errorbars pt 7 ps 0.25 title "measured data",\
tnl(x) title "nonlinear fit"
Auch diese Darstellung kann in einer Datei abgespeichert werden, wenn
zuvor das Grafikterminal entsprechend konfiguriert wurde.
Man kann auch alle notwendigen Berechnungen direkt von Gnuplot
ausführen lassen ohne vorher eine andere Software zu benutzen. Dazu
werden die Messwertpaare (x,t) in eine Datei mit 2 Spalten geschrieben
oder in Form einer inline Datei definiert und zur Berechnung aller
notwendigen Daten verwendet. Im weiteren müssen alle Werte in den
entsprechenden, gleichen Einheiten eingegeben werden. Als
Längeneinheit ergeben Millimeter und als Zeiteinheit Sekunden
sinnvolle Zahlenwerte.
$data << EOD
0. 41.45
0. 41.37
40. 40.74
40. 40.75
80. 39.97
80. 39.96
120. 39.13
120. 39.16
160. 38.31
160. 38.35
200. 37.48
200. 37.52
240. 36.59
240. 36.65
280. 35.69
280. 35.65
320. 34.70
320. 34.80
360. 33.85
360. 33.83
400. 32.87
400. 32.86
EOD
Desweiteren sind alle gemessenen Größen, die nicht in der
(x,t)-Tabelle enthalten sind, und deren Unsicherheiten als Variable zu
definieren. Dabei sind die gleichen Einheiten wie in der Datentabelle
zu verwenden. Alle im weiteren verwendeten Zahlenwerte sind
Beispielwerte und durch die Ergebnisse aus dem eigenen Experiment zu
ersetzen. Es werden die folgenden Werte benötigt:
- die Standardabweichung der Zeitmessung am Nullpunkt, die im
Teil1 des Versuchs bestimmt wurde
STDt=0.029
- dessen Auslenkung und deren Unsicherheit, die für alle
Messstellen x die gleiche sein sollte
a=84; ua=1
- die Anzahl der gemessenen Perioden
n=20
- die Größe
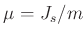 des Pendelkörpers aus Teil 1 des Versuches
des Pendelkörpers aus Teil 1 des Versuches
mu=320
Diese wird bei der Auswertung mittels linearer Ausgleichsrechnung
(Gleichung 6) vollständig vernachlässigt. Bei der
nichtlinearer Ausgleichsrechnung (Gleichung 7)
geht 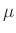 nur in den Korrekturterm der Pendellänge (Gleichung
5) ein. Da
nur in den Korrekturterm der Pendellänge (Gleichung
5) ein. Da 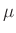 im Vergleich zu
im Vergleich zu 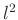 an allen Messtellen als
klein angesehen werden, wird hierbei der Einfluss von
an allen Messtellen als
klein angesehen werden, wird hierbei der Einfluss von 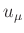 auf die
Unsicherheit von
auf die
Unsicherheit von 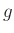 vernachlässigt.
vernachlässigt.
Nun können die zur Berechnung der verschiedenen Zwischenwerte notwendigen
Funktionen definiert werden.
- Zur Berechnung des Zeitmessfehlers
usysrUhr(t)=0.01+1/(24*3600)*t
ut(t)=STDt+usysrUhr(t)
- Für die Amplitudenreduktion
T0(x,t)=t/(1+a**2/16/(l0-x)**2)/n
uT0(x,t)=16*(l0-x)/(a**2+16*(l0-x)**2)**2\
*sqrt((2*a*(l0-x)*t*ua)**2+(2*a**2*t*ul0)**2\
+((l0-x)*(a**2+16*(l0-x)**2)*ut(t))**2)/n
- Zur Berechnung von
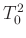 und der Unsicherheit
und der Unsicherheit 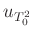
TQ(x,t)=T0(x,t)**2
uTQ(x,t)=2*T0(x,t)*uT0(x,t)
Danach werden die lineare Fitfunktion
tlin(x) = a1 + a2 * x
und die notwendigen Startwerte
a1= 4*pi**2*l0/9810
a2= -4*pi**2/9810
festgelegt. Bei den Startwerten wird von der physikalischen Bedeutung
der Parameter des linearen Modells (Gleichung6) und dem
bekannten Näherungswert für die Erdbeschleunigung ausgegangen. Bevor
der Fit-Prozedur mit
fit tlin(x) $data using 1:(TQ($1,$2)):(uTQ($1,$2)) yerr via a1,a2
gestartet wird, müssen die Einstellungen für die Ausgabe der
Ergebnisse der Fit-Prozedur analog zum Abschnitt4.1
vorgenommen werden. Die Ausgabe der Fitparameter, ihrer Unsicherheiten
und Kovarianz sowie die Berechnung und Ausgabe der gesuchten
Ergebnisse erfolgt genauso wie im Abschnitt4.1
beschrieben. Mit den verwendeten Daten ergibt sich aus dem Linearen Fit
-
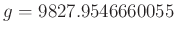 und
und
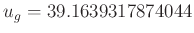 in
in 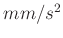
-
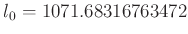 und
und
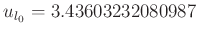 in
in 
Gerundet nach DIN 1333 ergibt das
-
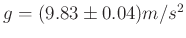
-
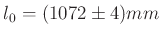
als Endergebnis. Die Erstellung der Grafik kann mit dem plot Befehl
plot $data using 1:(TQ($1,$2)):(uTQ($1,$2)) with errorbars pt 7 ps 0.25\
title "measured data", tlin(x) title "linear fit"
erfolgen. Zuvor sind die notwendigen Werte für die Wertebereiche und
Beschriftungen der Achsen entsprechend festzulegen.
Nachdem die festgelegten Wertebereiche xrange und yrange
für die Datenpunkte wieder zurückgesetzt wurden, kann die Fit Prozedur
für die nichtlineare Fitfunktion aufgerufen werden.
fit tnl(x) $data using 1:2 via a1,a2
Eine Gewichtung erfolgt hier nicht, da die Unsicherheiten
der Zeitmessung an allen Messstellen etwa gleich sind. Bevor der Fit
gestartet wird sind entsprechende Startwerte festzulegen. Die Ergebnisse
des Fits können wie oben beschrieben ausgegeben werden. Man erhält in
diesem Fall aus den angegebenen Daten
-
 und
und
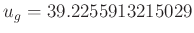 in
in 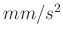
-
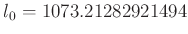 und
und
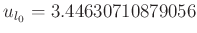 in
in 
Gerundet nach DIN 1333 ergibt das
-
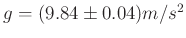
-
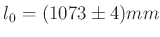
als Endergebnis. Die Darstellung der sich ergebenden Fitfunktion
zusammen mit den Daten und deren Unsicherheitsintervallen erfolgt mit
plot $data using 1:2:(ut($1)) with errorbars pt 7 ps 0.25\
title "measured data", tnl(x) title "nonlinear fit"
Die Wertebereiche und Beschriftungen sind wieder entsprechend festzulegen.
-
Physikalisches Grundpraktikum: Einführungspraktikum Seiten 6-8
Mathematisch-Naturwissenschaftliche FakultätI der HUB
Institut für Physik 2007
- http://gpr.physik.hu-berlin.de/Skripten/Einfuehrungspraktikum/PDF-Dateien/Einfuehrungspraktikum.pdf
abgerufen am 4.1.2016 11:02 Uhr
-
R.M. Dreizler und C.S. Lüdde
Theoretische Physik Band 1: Theoretische Mechanik
Springer 2008 ISBN 978-3-540-70557-4
- http://www.springer.com/de/book/9783540705574
abgerufen am 2.2.2018 17:39 Uhr
-
F. W. Bessel
Untersuchungen über die Länge des einfachen Secundenpendels
Abhandlungen der Königlichen Akademie der Wissenschaften zu Berlin
(1828)
Fußnoten
- ... werden1
- Das verwendete Pendel besteht aus einem Zylinder aus Blei
(Durchmesser 45mm Höhe 50mm), dessen Achse senkrecht zur
der Schwingungsachse ausgerichtet ist. Als Faden dient ein
Stahldraht (Durchmesser 0,5mm Länge 1000mm).
Eine Abschätzung mit dem GnuPlot-Skript
Fadenpendel.gnuplot
ergibt:
| Masse Faden |
1.543 |
g |
| m Pendelkörper |
901.933 |
g |
| Masse Pendel |
903.476 |
g |
| Schwerpunkt |
1024.103 |
mm |
| JS Faden |
128608.973 |
g
 |
| JS Pendelkörper |
301997.426 |
g
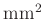 |
| JS Gesamt |
855253.881 |
g
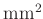 |
| JA Pendel |
948410.400 |
kg
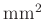 |
| mu Pendel |
946.625 |
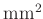 |
| lr mit Draht |
1025.027 |
mm |
| Vernachlässigung des Drahtes |
| Schwerpunkt |
1025.000 |
mm |
| m Pendelkörper |
901.933 |
g |
| JS Pendelkörper |
301997.426 |
g
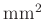 |
| JA Pendelkörper |
947895.964 |
kg
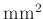 |
| mu Pendelkörper |
334.833 |
g
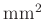 |
| lr ohne Draht |
1025.327 |
mm |
wobei die sich Aufhängung bei z=0 befindet. Man erkennt den
nur geringen Einfluss sowohl des Pendelkörpers als auch des Fadens auf
die reduzierten Pendellänge. Dabei ist der Effekt beider
Einflüsse gegenläufig. Prinzipiell lässt sich so ein Fadenpendel
konstruieren, für das gilt 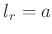 , wobei
, wobei 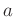 der Abstand des
Schwerpunktes des Massekörpers vom der Schwingungsachse ist .
der Abstand des
Schwerpunktes des Massekörpers vom der Schwingungsachse ist .
Peter Schaefer
2018-02-20
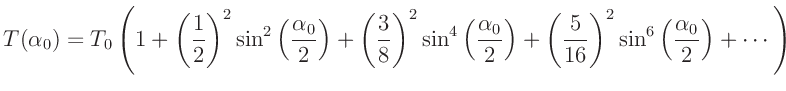
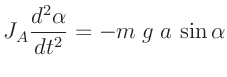
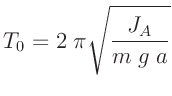
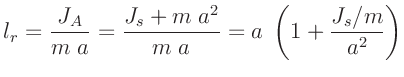
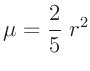
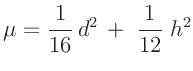
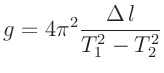
![]() verkürzt und
der Zusammenhang
verkürzt und
der Zusammenhang
![]() für
für ![]() Schwingungsperioden zur Auswertung benutzt.
Schwingungsperioden zur Auswertung benutzt.
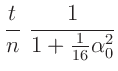 mit
mit  und
und 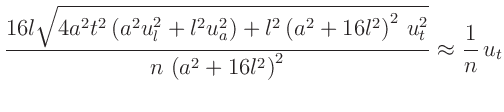
![]() für
für ![]() Perioden und der
Verkürzung des Pendelfadens
Perioden und der
Verkürzung des Pendelfadens ![]() (Gleichung7) für einen
nichtlinearen Fit genutzt werden. Die Einstellungen für die
Fit-Prozedur, die festlegen, in welcher Art und Weise die Ausgabe der
Ergebnisse erfolgt, sind die gleichen wie für den linearen Fit. Die zu
bestimmenden Parameter sind
(Gleichung7) für einen
nichtlinearen Fit genutzt werden. Die Einstellungen für die
Fit-Prozedur, die festlegen, in welcher Art und Weise die Ausgabe der
Ergebnisse erfolgt, sind die gleichen wie für den linearen Fit. Die zu
bestimmenden Parameter sind
![]() und
und
![]() . Auf den ersten Blick könnte man
auch den Wert von
. Auf den ersten Blick könnte man
auch den Wert von
![]() als möglichen
Fitparameter ansehen. Auf Grund der sich dann ergebenden sehr starken
Korrelationen zwischen diesen drei Parametern führt ein solcher Fit
nicht zu sinnvollen Ergebnissen. Damit kann die in den zwei gewählten
Parametern nichtlineare Modellfunktion
als möglichen
Fitparameter ansehen. Auf Grund der sich dann ergebenden sehr starken
Korrelationen zwischen diesen drei Parametern führt ein solcher Fit
nicht zu sinnvollen Ergebnissen. Damit kann die in den zwei gewählten
Parametern nichtlineare Modellfunktion
![]() des zylindrischen Pendelkörpers benötigt, der aus den
gemessenen Werten des Durchmessers und der Höhe berechnet wurde. Als
Startwerte für a1 und a2 können plausible Werte von
des zylindrischen Pendelkörpers benötigt, der aus den
gemessenen Werten des Durchmessers und der Höhe berechnet wurde. Als
Startwerte für a1 und a2 können plausible Werte von
![]() und der gemessene Schwerpunktabstand bei maximaler Pendellänge
genutzt werden, oder man verwendet die aus dem linearen Fit
berechneten Werte.
und der gemessene Schwerpunktabstand bei maximaler Pendellänge
genutzt werden, oder man verwendet die aus dem linearen Fit
berechneten Werte.