Auswertung Versuch F4-Federkonstante mit GnuPlot
Die gesuchte Federkonstante kann durch die schrittweise Belastung der
Feder mit Massestücken von ca. 50g ermittelt werden
(Einführungspraktikum (2007) Seite 9...11). Die aus der Belastung
resultierende Längenänderung wird als Position 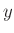 einer an der Feder
befestigten Marke mit Hilfe einer Spiegelskala gemessen (
1.Messreihe). Nach Erreichen der Höchstbelastung mit 8 Massestücken
wird die Feder wieder schrittweise entlastet und dabei die Position
der Marke erneut abgelesen (zweite Messreihe). Insgesamt werden so 15
Messwertepaare
einer an der Feder
befestigten Marke mit Hilfe einer Spiegelskala gemessen (
1.Messreihe). Nach Erreichen der Höchstbelastung mit 8 Massestücken
wird die Feder wieder schrittweise entlastet und dabei die Position
der Marke erneut abgelesen (zweite Messreihe). Insgesamt werden so 15
Messwertepaare 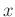
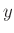 gewonnen. Die Unsicherheit der Positionen
gewonnen. Die Unsicherheit der Positionen 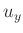 wird
durch den systematischen Restfehler der verwendeten Spiegelskala,
durch Fehler beim Ablesen von der Spiegelskala und durch die
Standardabweichung der verwendeten Massestücke bestimmt.
wird
durch den systematischen Restfehler der verwendeten Spiegelskala,
durch Fehler beim Ablesen von der Spiegelskala und durch die
Standardabweichung der verwendeten Massestücke bestimmt.
Aus dem Anstieg
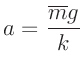 |
(1) |
der Geraden
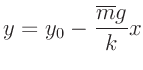 |
(2) |
kann dann die gesuchte Federkonstante berechnet werden. Hierbei
bedeuten 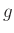 die Erdbeschleunigung,
die Erdbeschleunigung, 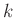 die gesuchte
Federkonstante,
die gesuchte
Federkonstante, 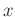 die Anzahl der Massestücke, mit denen die Feder
belastet wird. Die Größe
die Anzahl der Massestücke, mit denen die Feder
belastet wird. Die Größe 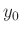 beschreibt die Position der verwendeten
Markierung bei unbelasteter Feder. Diese kann direkt nicht mit der
notwendigen Genauigkeit bestimmt werden, da die Achse der verwendeten
Feder im unbelasteten Zustand fertigungsbedingt leicht gebogen
ist. Das negative Vorzeichen resultiert aus der Tatsache, dass sich
der Nullpunkt der verwendeten Spiegelskala unten befindet und daher
die Werte von
beschreibt die Position der verwendeten
Markierung bei unbelasteter Feder. Diese kann direkt nicht mit der
notwendigen Genauigkeit bestimmt werden, da die Achse der verwendeten
Feder im unbelasteten Zustand fertigungsbedingt leicht gebogen
ist. Das negative Vorzeichen resultiert aus der Tatsache, dass sich
der Nullpunkt der verwendeten Spiegelskala unten befindet und daher
die Werte von 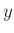 mit zunehmender Belastung abnehmen.
mit zunehmender Belastung abnehmen.
Um die so gewonnenen Daten mit
GnuPlot
oder
einer ähnlichen Software auszuwerten, ist als erstes die Erstellung
einer einfach Textdatei mit den Messdaten in tabellarischer Form
erforderlich. Die erste Spalte beinhaltet die Anzahl der Massestücke
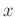 , die zweite Spalte die abgelesene Position
, die zweite Spalte die abgelesene Position 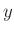 des Zeigers auf der
Spiegelskala (z.B. in mm) und die dritte Spalte den abgeschätzten
Fehler dieser Position
des Zeigers auf der
Spiegelskala (z.B. in mm) und die dritte Spalte den abgeschätzten
Fehler dieser Position 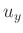 . Diese Spalte ist nur erforderlich, wenn
die Fehlerintervalle mit gezeichnet werden sollen oder eine Gewichtung
mit diesen Fehler erfolgen soll. Als Beispiel wird im weiteren die Datei
Messdaten-20150107-Platz2.txt
verwendet. Das Einlesen und Darstellen der Daten aus der vorbereiteter
Datei erfolgt durch Eingabe des Befehls:
. Diese Spalte ist nur erforderlich, wenn
die Fehlerintervalle mit gezeichnet werden sollen oder eine Gewichtung
mit diesen Fehler erfolgen soll. Als Beispiel wird im weiteren die Datei
Messdaten-20150107-Platz2.txt
verwendet. Das Einlesen und Darstellen der Daten aus der vorbereiteter
Datei erfolgt durch Eingabe des Befehls:
plot 'Messdaten-20150107-Platz2.txt' using 1:2
in das Terminalfenster von GnuPlot. Es sollte sich ein neues Fenster mit der
Darstellung der Messdaten öffnen. Als nächstes wird die
Fitfunktion im Terminalfenster definiert.
l(x) = y0 - a*x
Aus dem mit dem ersten Kommando erzeugten Plot können die für den
nachfolgenden Fit notwendigen Startwerte abgeschätzt und ebenfalls
eingegeben werden. Dieser Schritt ist für
GnuPlot
erforderlich, da es keine gesonderten Routinen für die Behandlung von
in den Parametern linearen Fitfunktionen gibt, die die gesuchten Parameter
mit Hilfe der Matrizenrechnung bestimmen. Daher müssen diese mit der
gleichen Routine bearbeitet werden wie in den Parametern nichtlineare
Fitfunktionen. Diese Vorgehensweise erfordert auch für lineare Modelle
die Vorgabe von Startwerten. Andere Software, wie z.B.
mathematica
stellen getrennte Routinen für lineare und nichtlineare Fitfunktionen
zur Verfügung.
y0=200
a=10.0
Nun kann der eigentliche Fit ausgeführt werden.
fit l(x) 'Messdaten-20150107-Platz2.txt' using 1:2 via y0,a
Im GnuPlot Terminalfenster werden der Verlauf der Iteration und die
numerischen Ergebnisse angezeigt. Die Fitfunktion kann zusammen mit
den Messdaten durch den Befehl
plot 'Messdaten-20150107-Platz2.txt' using 1:2, l(x)
gezeichnet werden.
Sofern bekannt, sind in der dritten Spalte der Messdatendatei die
Fehler 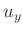 der Messwerte oder deren Abschätzungen eingetragen worden.
Diese können zur Darstellung von Fehlerbalken benutzt werden.
der Messwerte oder deren Abschätzungen eingetragen worden.
Diese können zur Darstellung von Fehlerbalken benutzt werden.
plot 'Messdaten-20150107-Platz2.txt' using 1:2:3 with errorbars
Liegen nur Abschätzungen zu der Größe der Messfehler vor, wie dies
in der überwiegenden Anzahl der Praktikumsversuche der Fall ist,
können diese nur zur Gewichtung der Messwerte verwendet werden. Dazu
muss die Option errorscaling gesetzt sein. Dies erfolgt mit:
set fit errorscaling
und entspricht der Grundeinstellung. In diesem Fall werden die Fehler
der Parameter mit dem reduzierten Wert von Chi-Quadrat skaliert. Dies
ist gleichbedeutend mit der Annahme, das die Standardabweichung der
Daten gleich der berechneten Standardabweichung des Fits ist. Dies
entspricht der üblichen statistischen Vorgehensweise.
Ist die Standardabweichung der Daten bekannt oder kann diese aus den
Messdaten an jedem Messpunkt auf der Grundlage einer ausreichenden
Anzahl von Messwerten bestimmt werden, kann durch
set fit noerrorscaling
die Vorgabeeinstellung geändert werden. In diesem Fall erfolgt die
Berechnung der Fehler der Parameter entsprechend dem
Fehlerfortpflanzungsgesetz aus den Fehlern der Messdaten. Nur in
diesem Fall kann der reduzierte Wert von Chi-Quadrat zur Beurteilung
der Güte des Fits herangezogen werden. Der mathematische Hintergrund
kann in den ,,Anmerkungen (2016)`` nachgelesen werden.
Der gewichtete Fit erfolgt mit dem Kommando:
fit l(x) 'Messdaten-20150107-Platz2.txt' using 1:2:3 yerr via y0,a
Danach kann das Ergebnis wieder mit
plot [0:9] 'Messdaten-20150107-Platz2.txt' using 1:2:3 with errorbars, l(x)
im Grafikfenster dargestellt und in einem geeigneten Grafikformat
exportiert werden.
Abbildung 1:
Messdaten und berechnete Ausgleichsgerade
|
Als letztes ist noch GnuPlot zu beenden:
quit
-
Physikalisches Grundpraktikum: Einführungspraktikum
Mathematisch-Naturwissenschaftliche FakultätI der HUB
Institut für Physik 2007
- http://gpr.physik.hu-berlin.de/Skripten/Einfuehrungspraktikum/PDF-Dateien/Einfuehrungspraktikum.pdf
abgerufen am 4.1.2016 11:02 Uhr
-
Rechnet QtiPlot falsch ?
Einige Anmerkungen zur Methode der linearen Regression
P. Schäfer
Institut für Physik, Humboldt-Universität zu Berlin 2016
- http://roe10.physik.hu-berlin.de/Grundpraktikum/Rechnet_QtiPlot_falsch/index.html
abgerufen am 21.3.2016 13:07 Uhr
Peter Schaefer
2016-03-29
![]() einer an der Feder
befestigten Marke mit Hilfe einer Spiegelskala gemessen (
1.Messreihe). Nach Erreichen der Höchstbelastung mit 8 Massestücken
wird die Feder wieder schrittweise entlastet und dabei die Position
der Marke erneut abgelesen (zweite Messreihe). Insgesamt werden so 15
Messwertepaare
einer an der Feder
befestigten Marke mit Hilfe einer Spiegelskala gemessen (
1.Messreihe). Nach Erreichen der Höchstbelastung mit 8 Massestücken
wird die Feder wieder schrittweise entlastet und dabei die Position
der Marke erneut abgelesen (zweite Messreihe). Insgesamt werden so 15
Messwertepaare ![]()
![]() gewonnen. Die Unsicherheit der Positionen
gewonnen. Die Unsicherheit der Positionen ![]() wird
durch den systematischen Restfehler der verwendeten Spiegelskala,
durch Fehler beim Ablesen von der Spiegelskala und durch die
Standardabweichung der verwendeten Massestücke bestimmt.
wird
durch den systematischen Restfehler der verwendeten Spiegelskala,
durch Fehler beim Ablesen von der Spiegelskala und durch die
Standardabweichung der verwendeten Massestücke bestimmt.
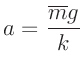
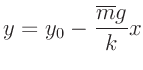
![]() , die zweite Spalte die abgelesene Position
, die zweite Spalte die abgelesene Position ![]() des Zeigers auf der
Spiegelskala (z.B. in mm) und die dritte Spalte den abgeschätzten
Fehler dieser Position
des Zeigers auf der
Spiegelskala (z.B. in mm) und die dritte Spalte den abgeschätzten
Fehler dieser Position ![]() . Diese Spalte ist nur erforderlich, wenn
die Fehlerintervalle mit gezeichnet werden sollen oder eine Gewichtung
mit diesen Fehler erfolgen soll. Als Beispiel wird im weiteren die Datei
Messdaten-20150107-Platz2.txt
verwendet. Das Einlesen und Darstellen der Daten aus der vorbereiteter
Datei erfolgt durch Eingabe des Befehls:
. Diese Spalte ist nur erforderlich, wenn
die Fehlerintervalle mit gezeichnet werden sollen oder eine Gewichtung
mit diesen Fehler erfolgen soll. Als Beispiel wird im weiteren die Datei
Messdaten-20150107-Platz2.txt
verwendet. Das Einlesen und Darstellen der Daten aus der vorbereiteter
Datei erfolgt durch Eingabe des Befehls:
![]() der Messwerte oder deren Abschätzungen eingetragen worden.
Diese können zur Darstellung von Fehlerbalken benutzt werden.
der Messwerte oder deren Abschätzungen eingetragen worden.
Diese können zur Darstellung von Fehlerbalken benutzt werden.