Die Gleichung 45 auf Seite 42 ist nur unter ganz bestimmten
Bedingungen gültig, da sie über die Fehlerfortpflanzung hergeleitet
wurde. Damit sie angewendet werden kann, müssen die Messdaten
beziehungsweise die Messunsicherheiten 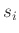 eine Reihe von
Anforderungen erfüllen:
eine Reihe von
Anforderungen erfüllen:
- Die Messunsicherheiten
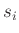 sind echte, experimentell bestimmte
Messunsicherheiten, die zum Beispiel durch mehrfache
Wiederholungsmessung an der jeweiligen Messstelle
sind echte, experimentell bestimmte
Messunsicherheiten, die zum Beispiel durch mehrfache
Wiederholungsmessung an der jeweiligen Messstelle 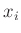 ermittelt
wurden. Als Werte
ermittelt
wurden. Als Werte 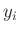 sind dann die jeweiligen Mittelwerte zu
verwenden.
sind dann die jeweiligen Mittelwerte zu
verwenden.
- Die Verteilungsfunktion der Messunsicherheiten an jeder
Messstelle
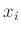 ist eine Normalverteilung mit dem Erwartungswert 0
und der Varianz
ist eine Normalverteilung mit dem Erwartungswert 0
und der Varianz 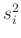 .
.
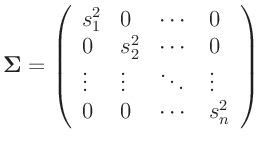
- Die Messunsicherheiten der einzelnen Messstellen sind
unkorreliert, die Kovarianzmatrix
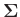 der Messwerte
der Messwerte 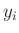 ist eine Diagonalmatrix.
ist eine Diagonalmatrix.
- Die Modellfunktion ist linear in den Parametern und die
Basisfunktionen sind an den gegebenen Messpositionen
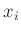 linear
unabhängig. Dieser Punkt ist beim hier betrachteten
Geradenausgleich (ein Spezialfall der linearen Regression) erfüllt.
linear
unabhängig. Dieser Punkt ist beim hier betrachteten
Geradenausgleich (ein Spezialfall der linearen Regression) erfüllt.
Unter diesen Voraussetzungen genügt die Summe der Abweichungsquadrate
einer 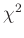 -Verteilung mit dem Erwartungswert
-Verteilung mit dem Erwartungswert
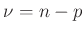 und der
Varianz
und der
Varianz 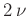 . Die Anzahl der Parameter
. Die Anzahl der Parameter 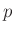 ist im Fall des
hier beschriebenen einfachen Geradenausgleichs gleich 2.
ist im Fall des
hier beschriebenen einfachen Geradenausgleichs gleich 2. 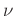 gibt
die Anzahl der Freiheitsgrade (degrees of freedom, oftmals
abgekürzt mit dof) an. Der Wert von
gibt
die Anzahl der Freiheitsgrade (degrees of freedom, oftmals
abgekürzt mit dof) an. Der Wert von
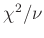 kann unter den oben
genannten und nur unter diesen Bedingungen als ein Test für die Güte
der Anpassung des Modells, in diesem Fall eine Gerade, an die Daten
genutzt werden. Liegt der Wert von
kann unter den oben
genannten und nur unter diesen Bedingungen als ein Test für die Güte
der Anpassung des Modells, in diesem Fall eine Gerade, an die Daten
genutzt werden. Liegt der Wert von
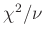 im Intervall
im Intervall
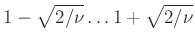 kann das gewählte Modell,
hier die Gerade, vom Standpunkt der klassischen Statistik nicht
verworfen werden (Hogg (2010) Anmerkung 32). Dieser Test
besticht durch seine Einfachheit, ist aber nicht unproblematisch
(siehe dazu: (Andrae (2010)).
kann das gewählte Modell,
hier die Gerade, vom Standpunkt der klassischen Statistik nicht
verworfen werden (Hogg (2010) Anmerkung 32). Dieser Test
besticht durch seine Einfachheit, ist aber nicht unproblematisch
(siehe dazu: (Andrae (2010)).
In vielen Fällen ist im Praktikum die 1.Forderung an die Messdaten
nicht erfüllt, man kann aber davon ausgehen, dass die
Messunsicherheiten an allen Messstellen mit der gleichen Varianz
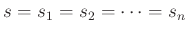 beschreiben werden. Diese ist damit auch unabhängig von der Größe des
Messwerts
beschreiben werden. Diese ist damit auch unabhängig von der Größe des
Messwerts 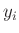 . Dies ist zum Beispiel beim Ablesen auf einer
einfachen Längenskala (Büromaßstab, Stahllineal, Spiegelskala) der
Fall. Dann können die Gleichungen 49 und 50 auf Seite 42 angewandt
werden, wobei für die unbekannte Varianz
. Dies ist zum Beispiel beim Ablesen auf einer
einfachen Längenskala (Büromaßstab, Stahllineal, Spiegelskala) der
Fall. Dann können die Gleichungen 49 und 50 auf Seite 42 angewandt
werden, wobei für die unbekannte Varianz 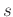 der Messunsicherheit
deren Schätzwert
der Messunsicherheit
deren Schätzwert
zu verwenden ist.
Ist davon auszugehen, dass die unbekannten Messunsicherheiten an den
einzelnen Messstellen deutliche verschieden sind, oder dass die
Messunsicherheiten eine deutliche Abhängigkeit vom gemessen Wert
erwarten lassen, ist die obige Annahme der Gleichheit der Varianzen
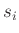 nicht mehr gegeben. Die Methode der linearen Regression
erfordert in diesem Fall die Einführung von Gewichten
nicht mehr gegeben. Die Methode der linearen Regression
erfordert in diesem Fall die Einführung von Gewichten 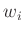 . Es wird
das Minimum der Größe
. Es wird
das Minimum der Größe
bestimmt. Für die Festlegung der Gewichte gibt es eine Vielzahl
verschiedener Möglichkeiten (siehe dazu Strutz (2016), Chapter
3). In einigen Fällen liegen Informationen darüber vor, wie sich die
einzelnen Messunsicherheiten relativ zueinander verhalten. Dies ist
z.B. bei Messungen mit elektrischen oder elektronischen Messgeräten,
die über mehrere verschiedene Messbereiche verfügen, der Fall
(Einführungsskript (2007) Seite 19 ff.). An Hand der zu den
einzelnen Messbereichen angegebenen Messunsicherheiten 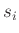 können
die Gewichte
können
die Gewichte
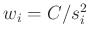 festgelegt werden. Hierbei ist
festgelegt werden. Hierbei ist 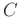 eine
willkürlich festlegbare Konstante. Diese Vorgehensweise
ist analog zu der im Abschnitt 3.8 (Seite 47) beschriebenen Gewichtung
für die Bildung eines gewichteten Mittelwertes. In vielen Fällen
erhalten so alle im selben Messbereich gemessenen Werte jeweils das
gleiche Gewicht. In all den Fällen, in denen die Parameter
eine
willkürlich festlegbare Konstante. Diese Vorgehensweise
ist analog zu der im Abschnitt 3.8 (Seite 47) beschriebenen Gewichtung
für die Bildung eines gewichteten Mittelwertes. In vielen Fällen
erhalten so alle im selben Messbereich gemessenen Werte jeweils das
gleiche Gewicht. In all den Fällen, in denen die Parameter 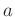 und
und 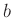 unter Anwendung einer Gewichtung, berechnet wurden, lautet die
Gleichung 45 auf Seite 42 richtig:
unter Anwendung einer Gewichtung, berechnet wurden, lautet die
Gleichung 45 auf Seite 42 richtig:
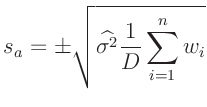 und und 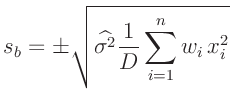 |
(45) |
In diesem Fall ist für die unbekannte Varianz deren Schätzwert
zu verwenden. Der mathematische Hintergrund kann in Schäfer (2016)
und Martin (2012) (Seite 149 -151 Chapter 8.1.2 insbesondere Gleichung 8.33)
nachgelesen werden. Damit die so bestimmten Fehlerintervalle richtig
sind, ist die Erfüllung der beiden oben benannten Forderungen nach
Normalverteilung der unbekannten Messunsicherheiten und dass die
einzelnen Messunsicherheiten unkorreliert sind zwingend notwendig
(siehe hierzu Andrae (2010)).
Zum Abschnitt 3.8 ,,Gewichtetes Mittel`` (Seite 47)
sind einige ergänzende Bemerkungen notwendig. Die Formel für 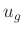 in Gleichung 56
in Gleichung 56
liefert immer einen Wert für 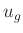 , der kleiner ist, als der
kleinste Wert von
, der kleiner ist, als der
kleinste Wert von 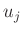 . Die Anwendung dieser Formel setzt voraus, dass
alle Werte
. Die Anwendung dieser Formel setzt voraus, dass
alle Werte 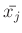 als Ergebnis jeweils einer Stichprobe aus der
gleichen Grundgesamtheit angesehen werden können. Auf diesen Umstand
wird in in der Herleitung in Bevington (2003) (Chapter 4,
Seite 56) ausdrücklich hingewiesen. Nur wenn alle Unsicherheiten
einen gemeinsamen Bereich überdecken, kann davon ausgegangen werden,
dass diese Voraussetzung erfüllt ist. Nach James (2006)
(Chapter 11.5.2, S 323-325) lässt sich mit:
als Ergebnis jeweils einer Stichprobe aus der
gleichen Grundgesamtheit angesehen werden können. Auf diesen Umstand
wird in in der Herleitung in Bevington (2003) (Chapter 4,
Seite 56) ausdrücklich hingewiesen. Nur wenn alle Unsicherheiten
einen gemeinsamen Bereich überdecken, kann davon ausgegangen werden,
dass diese Voraussetzung erfüllt ist. Nach James (2006)
(Chapter 11.5.2, S 323-325) lässt sich mit:
testen, ob diese Voraussetzung erfüllt ist. Dabei ist
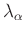 das Quantil der
das Quantil der 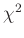 -Verteilung mit
-Verteilung mit 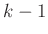 Freiheitsgraden für das Signifikanzniveau
Freiheitsgraden für das Signifikanzniveau 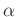 . Für das im
Praktikum benutzte Signifikanzniveau
. Für das im
Praktikum benutzte Signifikanzniveau
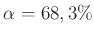 gilt
gilt
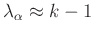 .
Wenn diese Testbedingung erfüllt ist, wird das mit Gleichung 55
bestimmte gewichtete Mittel in dem Bereich liegen, der von allen
Unsicherheitsintervallen überdeckt wird und dessen Unsicherheit kann
mit Gleichung 56 berechnet werden. Das in Abbildung 15 gezeigte
Beispiel erfüllt diese Voraussetzung nicht. Die
Unsicherheitsintervalle überdecken sich nur paarweise. Unter solchen
Bedingungen führt die Anwendung der Gleichung 56 zu einem falschen
Ergebnis.
.
Wenn diese Testbedingung erfüllt ist, wird das mit Gleichung 55
bestimmte gewichtete Mittel in dem Bereich liegen, der von allen
Unsicherheitsintervallen überdeckt wird und dessen Unsicherheit kann
mit Gleichung 56 berechnet werden. Das in Abbildung 15 gezeigte
Beispiel erfüllt diese Voraussetzung nicht. Die
Unsicherheitsintervalle überdecken sich nur paarweise. Unter solchen
Bedingungen führt die Anwendung der Gleichung 56 zu einem falschen
Ergebnis.
Soll aus Messungen der gleichen physikalischen Größe, die mit
unterschiedlichen Messmethoden bestimmt wurden und damit nicht
als der gleichen Grundgesamtheit entstammend angesehen werden
können, ein Gesamtergebnis ermittelt werden, muss man die Streuung
der einzelnen Werte mit berücksichtigen. Dies ist zum Beispiel beim
Versuch E12 ,,Elektronen in Feldern`` der Fall. Hier
wird die spezifische Ladung 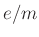 des Elektrons mit drei
verschiedenen Methoden bestimmt.
des Elektrons mit drei
verschiedenen Methoden bestimmt.
Das gewichtete Mittel kann genauso wie die lineare Regression als
ein spezieller Fall des allgemeinen linearen Modells 1angesehen werden. Für den Wert des gewichteten Mittels 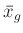 ergibt sich
daraus der in Gleichung 55 angegebene Ausdruck. Für die Varianz
ergibt sich
daraus der in Gleichung 55 angegebene Ausdruck. Für die Varianz
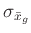 dieses Wertes folgt aber:
dieses Wertes folgt aber:
Diese Beziehung findet man auch bei Bevington (2003) (Chapter 4,
Seite 58, Gleichung 4.23) für die Varianz des gewichteten Mittels,
wenn dies mit Hilfe relativer Unsicherheiten berechnet wird.
Daraus ergibt sich für die Unsicherheit 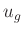 des gewichteten Mittels
des gewichteten Mittels
In diesem Ausdruck werden die Abweichungen der einzelnen Werte
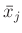 vom gemeinsamen Mittelwert
vom gemeinsamen Mittelwert 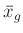 mit
berücksichtigt. Wenn der obengenannte Test nicht positiv ausfällt,
ist der so bestimmte Wert für
mit
berücksichtigt. Wenn der obengenannte Test nicht positiv ausfällt,
ist der so bestimmte Wert für 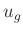 größer als der nach Gleichung 56
berechnete.
größer als der nach Gleichung 56
berechnete.
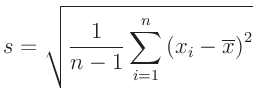
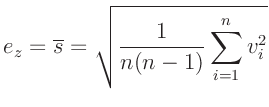
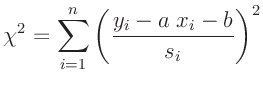
![]() beschreiben werden. Diese ist damit auch unabhängig von der Größe des
Messwerts
beschreiben werden. Diese ist damit auch unabhängig von der Größe des
Messwerts ![]() . Dies ist zum Beispiel beim Ablesen auf einer
einfachen Längenskala (Büromaßstab, Stahllineal, Spiegelskala) der
Fall. Dann können die Gleichungen 49 und 50 auf Seite 42 angewandt
werden, wobei für die unbekannte Varianz
. Dies ist zum Beispiel beim Ablesen auf einer
einfachen Längenskala (Büromaßstab, Stahllineal, Spiegelskala) der
Fall. Dann können die Gleichungen 49 und 50 auf Seite 42 angewandt
werden, wobei für die unbekannte Varianz ![]() der Messunsicherheit
deren Schätzwert
der Messunsicherheit
deren Schätzwert
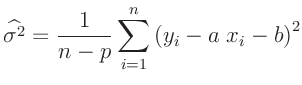
![]() nicht mehr gegeben. Die Methode der linearen Regression
erfordert in diesem Fall die Einführung von Gewichten
nicht mehr gegeben. Die Methode der linearen Regression
erfordert in diesem Fall die Einführung von Gewichten ![]() . Es wird
das Minimum der Größe
. Es wird
das Minimum der Größe
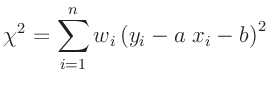
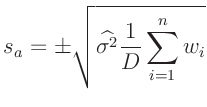 und
und 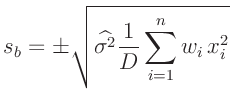
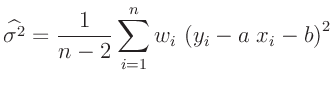
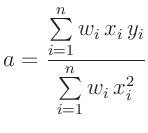 und
und 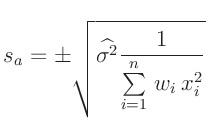
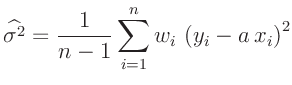
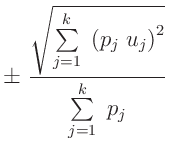 mit
mit 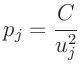
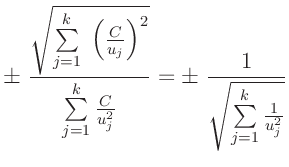
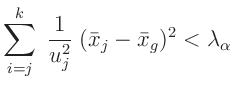
![]() des Elektrons mit drei
verschiedenen Methoden bestimmt.
des Elektrons mit drei
verschiedenen Methoden bestimmt.
![]() ergibt sich
daraus der in Gleichung 55 angegebene Ausdruck. Für die Varianz
ergibt sich
daraus der in Gleichung 55 angegebene Ausdruck. Für die Varianz
![]() dieses Wertes folgt aber:
dieses Wertes folgt aber:
![$\displaystyle \sigma_{\bar{x}_g} = \frac{1}{n-1}\left[\frac{\sum\limits_{j=1}^n\;p_j\,x_j^2}{\sum\limits_{i=j}^n\;p_j}\;
-\;\bar{x}_g^2\right]
$](img97.png)
![$\displaystyle u_g=\pm\,\sqrt{\sigma_{\bar{x}_g}}=\pm\,\sqrt{\frac{1}{n-1}\left[...
...j=1}^n\;p_j\,\bar{x}_j^2}{\sum\limits_{i=j}^n\;p_j}\;
-\;\bar{x}_g^2\right]}
$](img99.png)