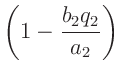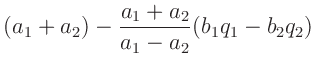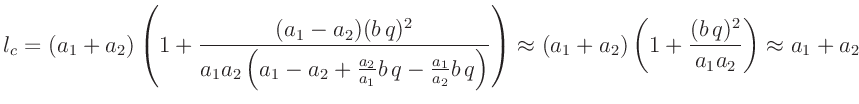Versuch M9-Reversionspendel
Ziel des Versuches M9 (zu Details sei auf Physikalisches Grundpraktikum: Mechanik und Thermodynamik (2012)
verwiesen) ist die Ermittlung der Erdbeschleunigung am
Standort Berlin Adlershof mit Hilfe eines Reversionspendels. Die Idee,
dafür ein Pendel mit reziproken Achsen zu benutzen, wurde erstmals von
J.G.F.Bohnenberger (1811) publiziert. Das erste Reversionspendel
wurde von H.Kater (1818) konstruiert und für Messungen
eingesetzt. Über mehr als 150 Jahre, bis Ende der sechziger Jahre des
letzten Jahrhunderts, wurden Reversionspendel zur Absolutbestimmung der
Erdbeschleunigung verwendet. Bei den 1969 in Potsdam durchgefährten
Messung wurde  mit
mit
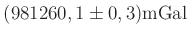 bestimmt (J.Höpfner (2012)). Dies waren die genausten
Messungen, die mit Reversionspendeln durchgefährt wurden. In
den folgenden Jahren wurden sie von den noch präziseren
Fallgravimetern abgelöst.
bestimmt (J.Höpfner (2012)). Dies waren die genausten
Messungen, die mit Reversionspendeln durchgefährt wurden. In
den folgenden Jahren wurden sie von den noch präziseren
Fallgravimetern abgelöst.
Mit einem solchen Pendel reduziert sich die gestellte Aufgabe
auf die Messung des Abstandes der beiden Achsen, welcher der Länge
eines gleich schwingenden mathematischen Pendels entspricht, und die
Bestimmung der für beide Achsen identischen Periodendauer.
Als Messgeräte stehen im Praktikum ein Anbaumessschieber und eine
elektronische, durch eine Lichtschranke gesteuerte Stoppuhr zur
Verfügung. Der systematische Restfehler des verwendeten
Längenmessgerätes beträgt nach den Angaben des Herstellers
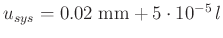 . Der aus zehnmaliger
Wiederholung der Messung bestimmte zufällige Fehler, der
Vertrauensbereich des ermittelten Mittelwertes, beträgt meist weniger
als
. Der aus zehnmaliger
Wiederholung der Messung bestimmte zufällige Fehler, der
Vertrauensbereich des ermittelten Mittelwertes, beträgt meist weniger
als
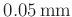 . Der daraus resultierende relative
Gesamtfehler
. Der daraus resultierende relative
Gesamtfehler 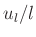 der Längenmessung liegt bei einem
Schneidenabstand des Reversionspendels von
der Längenmessung liegt bei einem
Schneidenabstand des Reversionspendels von
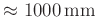 unter
unter
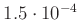 . Dies wird auch durch die Standardabweichung der von
den Studenten in den vergangenen Jahren an den einzelnen Messplätzen
ermittelten Werte für den Schneidenabstand untermauert, die unter
. Dies wird auch durch die Standardabweichung der von
den Studenten in den vergangenen Jahren an den einzelnen Messplätzen
ermittelten Werte für den Schneidenabstand untermauert, die unter
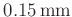 liegt.
liegt.
Die von der Elektronikwerkstatt des Instituts für Physik gebauten, von
einer Lichtschranke gesteuerten
Stoppuhren nutzen als Zeitnormal einen thermisch stabilisierten
Schwingquarz mit einer Sollfrequenz von 1MHz. Die gemessene
Frequenzabweichung ist kleiner als 1Hz. Die Zeitauflösung der
Digitalanzeige beträgt 1ms. Daraus ergibt sich ein systematischer
Restfehler für die Zeitmessung von
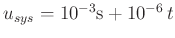 .
Für die Bestimmung von g wird die Zeitdauer von 40 Schwingungen,
.
Für die Bestimmung von g wird die Zeitdauer von 40 Schwingungen,
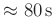 , mit zehnmaliger Wiederholung gemessen.
Für jede Wiederholung wird das Pendel neu ausgelenkt.
Die daraus Standardabweichung ist kleiner als
, mit zehnmaliger Wiederholung gemessen.
Für jede Wiederholung wird das Pendel neu ausgelenkt.
Die daraus Standardabweichung ist kleiner als
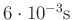 .
Daraus resultiert ein relativer Fehler der Zeitmessung
.
Daraus resultiert ein relativer Fehler der Zeitmessung 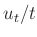 von
von
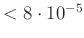 .
.
Mit den zur Verfügung stehenden Messgeräten sollte der Wert von g mit
einem relativen Fehler von besser als
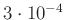 , das heißt mit
einem absoluten Fehler von besser als
, das heißt mit
einem absoluten Fehler von besser als
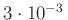 ms
ms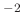 bestimmbar sein. Die Ergebnisse
der letzten Jahre zeigen, dass diese Genauigkeit in den meisten Fällen
auch erreicht wird. Allerdings liegen die bestimmten Werte von g
systematisch, zum Teil um das Mehrfache des Fehlerintervalls, über dem
Referenzwert der Physikalisch-Technischen Bundesanstalt für Berlin
Adlershof. Es werden mit hoher Genauigkeit falsche Werte
bestimmt, ohne dass die Ursache für diese Abweichungen bekannt ist.
bestimmbar sein. Die Ergebnisse
der letzten Jahre zeigen, dass diese Genauigkeit in den meisten Fällen
auch erreicht wird. Allerdings liegen die bestimmten Werte von g
systematisch, zum Teil um das Mehrfache des Fehlerintervalls, über dem
Referenzwert der Physikalisch-Technischen Bundesanstalt für Berlin
Adlershof. Es werden mit hoher Genauigkeit falsche Werte
bestimmt, ohne dass die Ursache für diese Abweichungen bekannt ist.
Das im Versuch M9 verwendete Reversionspendel (Abbildung
1) ist nur aus einem Material gefertigt. Es besteht aus
einem ca 1.5m langen Stahlstab mit 16mm Durchmesser. An diesem
sind die zwei Schneiden mit einem Abstand von ca 0.98m
angebracht. In der Nähe des einen Endes ist das eine Massenstück
befestigt. Das zweite Massenstück lässt sich beliebig zwischen den
beiden Schneiden positionieren um damit die Lage des Schwerpunktes
einzustellen.
Abbildung 1:
Reversionspendel
![\begin{figure}\centering
%
\includegraphics[width=84.1mm]{Abbildung-1}
\end{figure}](Timg19.png) |
Im weiteren werden der Schneidenabstand mit 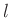 , der Abstand des
Schwerpunktes von der Schneide 1 mit
, der Abstand des
Schwerpunktes von der Schneide 1 mit 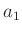 und der Abstand des
Schwerpunktes von der Schneide 2 mit
und der Abstand des
Schwerpunktes von der Schneide 2 mit 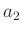 bezeichnet. Damit gilt
bezeichnet. Damit gilt
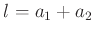 .
.
Die Massen der einzelnen Teile wurden
so gewählt, dass es zwei Positionen gibt, an denen die
Schwingungsdauern für beide Schneiden gleich sind.
Abbildung 2:
Berechnete Abhängigkeit der Periodendauer von der
Position des Laufgewichtes, angegeben in Ringmarken.
![\begin{figure}\centering
%
\includegraphics[width=93mm]{TversusX}
\end{figure}](Timg24.png) |
Abbildung 3:
Berechnete Abhängigkeit der Trägheitsmomente von der
Position des Laufgewichtes, angegeben in Ringmarken.
![\begin{figure}\centering
%
\includegraphics[width=93mm]{JversusX}
\end{figure}](Timg25.png) |
In Abbildung 2 ist die mit dem GnuPlot-Skript
Reversionspendel.gnuplot
berechnete Abhängigkeit der Periodendauer von der Stellung des
Laufgewichtes für das verwendete Reversionspendel dargestellt. Um die
Position des Laufgewichtes zu bestimmen, ist der Pendelstab im Abstand
von 20mm mit eingedrehten Marken versehen. Der Nullpunkt dieser
Skala liegt in etwa an der Position der Schneide 2. Damit kann der
Abstand der Kante des Laufgewichts von der Schneide 2 reproduzierbar
in Schritten von einer Ringmarke eingestellt werden.
Die Schnittpunkte der beiden Kurven liegen etwa bei 7 und etwa bei 36.5
Ringmarken. In der einen Position sind die beiden Massestücke
weit auseinander. Wie Abbildung 3 zeigt, ist das daraus
resultierende auf den Schwerpunkt bezogene Trägheitsmoment 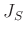 groß. In der anderen Position
ist der Abstand der beiden Massestücke klein und das Trägheitsmoment
groß. In der anderen Position
ist der Abstand der beiden Massestücke klein und das Trägheitsmoment
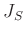 ist geringer. Noch stärker unterscheiden sich die Werte von
ist geringer. Noch stärker unterscheiden sich die Werte von 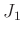 .
Bei großen Trägheitsmomenten ist die Pendelschwingung stabiler und
reagiert weniger empfindlich auf Störungen. Beim ersten Schnittpunkt
beträgt der Abstand
.
Bei großen Trägheitsmomenten ist die Pendelschwingung stabiler und
reagiert weniger empfindlich auf Störungen. Beim ersten Schnittpunkt
beträgt der Abstand 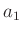 der Schneide 1 vom Schwerpunkt
der Schneide 1 vom Schwerpunkt
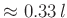 . Dies entspricht etwa dem Wert den
F.W.Bessel (1850) angibt. Für den zweiten Schnittpunkt ist
dieser Abstand mit
. Dies entspricht etwa dem Wert den
F.W.Bessel (1850) angibt. Für den zweiten Schnittpunkt ist
dieser Abstand mit
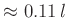 wesentlich kleiner. Aus diesen
Gründen sollte die Einstellung mit dem größeren Abstand der
Massestücke verwendet werden.
wesentlich kleiner. Aus diesen
Gründen sollte die Einstellung mit dem größeren Abstand der
Massestücke verwendet werden.
Mit vertretbarem Aufwand ist es nicht möglich, einen der beiden
Schnittpunkte exakt einzustellen. Der genaue Wert der Periodendauer
kann nur aus einer möglichst dichten Annäherung an den gesuchten
Schnittpunkt bestimmt werden. Dafür gibt es zwei verschiedene Wege.
Hat man auf jeder Seite des Schnittpunktes eine Position des
Laufgewichtes gefunden, bei der sich die gemessenen Periodendauern für
beide Schneiden nur geringfügig unterscheiden, können anstelle der
genauen Funktionen der Kurvenäste die jeweiligen Sekanten für die
Berechnung des Schnittpunktes genutzt werden. Dazu werden paarweise die
Abbildung 4:
Bestimmung von 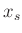 und
und 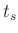 aus dem Schnittpunkt der
beiden Kurven
aus dem Schnittpunkt der
beiden Kurven
![\begin{figure}\centering
%
\includegraphics[width=93mm]{AbbSchnittpunkt}
\end{figure}](Timg36.png) |
Punkte
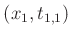 und
und
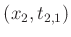 sowie
sowie
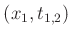 und
und
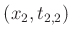 durch Geraden verbunden. Dabei bezeichnet der erste
Index die Position des Laufgewichtes. Der zweite Index steht für die
jeweilige Schneide. Der Schnittpunkt der beiden Geraden ist dann
gegeben durch:
durch Geraden verbunden. Dabei bezeichnet der erste
Index die Position des Laufgewichtes. Der zweite Index steht für die
jeweilige Schneide. Der Schnittpunkt der beiden Geraden ist dann
gegeben durch:
Auf Grund der konvexen Krümmung der beiden Funktion liegt der so
berechnete Wert von 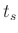 immer oberhalb des Schnittpunktes der beiden
Kurven.
immer oberhalb des Schnittpunktes der beiden
Kurven.
F.W.Bessel (1828) hatte gezeigt, dass es nicht notwendig
ist, genau gleiche Schwingungszeiten für beide Schneiden experimentell
einzustellen1.
Die Schwingungsdauer eines Pendels 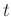 , dessen mathematische
Länge dem Schneidenabstand entspricht, lässt sich aus den gemessenen
Schwingungszeiten um die beiden Schneiden
, dessen mathematische
Länge dem Schneidenabstand entspricht, lässt sich aus den gemessenen
Schwingungszeiten um die beiden Schneiden 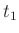 und
und 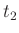 und den
entsprechenden Schwerpunktabständen
und den
entsprechenden Schwerpunktabständen 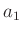 und
und 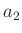 theoretisch
berechnen.
theoretisch
berechnen.
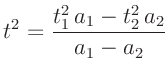 |
(2) |
Diese Gleichung2 ist für die praktische Anwendung nicht sonderlich
zweckmäßig, da sie die Bestimmung beider Schwerpunktabstände mit hoher
Genauigkeit erfordert.
Bei F.W.Bessel (1828) ist auf Seite 98 eine Gleichung
für die Länge des einfachen Sekundenpendels 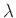 angegeben, die
für ein symmetrisches, inhomogenes Reversionspendel hergeleitet wurde.
Die dort schon enthaltenen Korrekturen für den Luftauftrieb und
für den Einfluss der mitschwingenden Luftmasse gelten so nicht für ein
homogenes, asymmetrisches Reversionspendel. Lässt man in dieser
Gleichung auch die sehr kleinen Korrekturen für Verschiebung der
Schneiden auf der Unterlage und die Änderung der Luftdichte während
der Messung von
angegeben, die
für ein symmetrisches, inhomogenes Reversionspendel hergeleitet wurde.
Die dort schon enthaltenen Korrekturen für den Luftauftrieb und
für den Einfluss der mitschwingenden Luftmasse gelten so nicht für ein
homogenes, asymmetrisches Reversionspendel. Lässt man in dieser
Gleichung auch die sehr kleinen Korrekturen für Verschiebung der
Schneiden auf der Unterlage und die Änderung der Luftdichte während
der Messung von 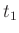 und
und 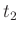 unberücksichtigt,
so ergibt sich daraus für die Schwingungsdauer des
Reversionspendels:
unberücksichtigt,
so ergibt sich daraus für die Schwingungsdauer des
Reversionspendels:
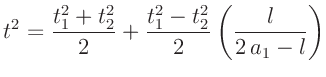 |
(3) |
wobei 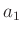 der Abstand des Schwerpunktes von der Schneide 1 und
der Abstand des Schwerpunktes von der Schneide 1 und
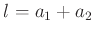 der Abstand der beiden Scheiden ist.
Diese Gleichung lässt sich allgemein für jedes Reversionspendel
herleiten3.
Für den Fall, dass die Differenz zwischen den Schwingungsdauern der beiden
Schneiden ausreichend klein ist, werden an die Genauigkeit, mit der
der Schwerpunktabstand
der Abstand der beiden Scheiden ist.
Diese Gleichung lässt sich allgemein für jedes Reversionspendel
herleiten3.
Für den Fall, dass die Differenz zwischen den Schwingungsdauern der beiden
Schneiden ausreichend klein ist, werden an die Genauigkeit, mit der
der Schwerpunktabstand 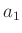 bestimmt werden muss, keine hohen
Anforderungen gestellt.
bestimmt werden muss, keine hohen
Anforderungen gestellt.
Die Schwingungsgleichung für ein ungedämpftes physikalisches Pendels lautet:
Als Lösung erhält man ein vollständiges elliptisches Integral erster Art:
Dieses kann durch eine Reihenentwicklung gelöst werden und fährt auf:
Die vollständige Herleitung findet man zum Beispiel in
R.M.Dreizler, C.S.Lüdde (2008) (Kapitel 4.2.1, Seiten 162-169). Erfolgt die
Messung bei hinreichend kleinen Amplituden kann dieser Ausdruck durch
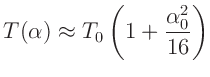 |
(4) |
angenähert werden. Bei dem oben abgeschätzten systematischen Restfehler der
verwendeten Uhr sollte 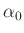 kleiner als 0.2 (entspricht etwa
kleiner als 0.2 (entspricht etwa
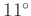 ) sein, damit der durch die Kleinwinkelnäherung und durch den
Abbruchterm entstehende Gesamtfehler den Wert von
) sein, damit der durch die Kleinwinkelnäherung und durch den
Abbruchterm entstehende Gesamtfehler den Wert von
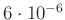 nicht übersteigt.
nicht übersteigt.
Um den Einfluss der Dämpfung auf die Schwingung eines physikalisches
Pendels zu beschreiben, müsste die Schwingungsgleichung
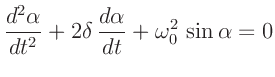 mit
mit 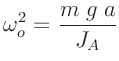
gelöst werden. 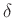 ist die Abklingkonstante. Im Fall schwacher
Dämpfung kann die zeitliche Abnahme der Schwingungsamplitude durch ein
Exponentialfunktion beschrieben werden.
ist die Abklingkonstante. Im Fall schwacher
Dämpfung kann die zeitliche Abnahme der Schwingungsamplitude durch ein
Exponentialfunktion beschrieben werden.
Aus der am Messplatz 2 beobachteten Abnahme der Amplitude über einen
Zeitraum von 90 Minuten ergibt sich, dass 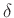 ungefähr bei
ungefähr bei
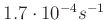 liegt.
liegt.
Für derart kleine Werte der Abklingkonstante ist die vollständige
Lösung der Schwingungsgleichung nicht notwendig. Die folgende
Betrachtungsweise ist ausreichend.
Zum einen gilt für die Kreisfrequenz einer gedämpften harmonischen
Schwingung:
Für den vorliegenden Fall sehr kleiner Dämpfung
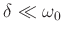 ergibt sich daraus für die Periodendauer einer harmonischen Schwingung
ergibt sich daraus für die Periodendauer einer harmonischen Schwingung
Die sich aus dem bestimmten Wert von 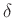 ergebende relative Änderung
von
ergebende relative Änderung
von 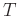 bleibt unter
bleibt unter
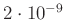 und kann daher im weiteren
vernachlässigt werden.
und kann daher im weiteren
vernachlässigt werden.
Zum anderen ist die Periodendauer eines Pendels aber nach Gleichung
4 von der Schwingungsamplitude abhängig und wird bei zeitlich
abnehmender Amplitude eine Funktion der Messzeit 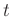 .
.
Für die über die Zeit von n Perioden gemittelte Periodendauer 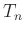 erhält man4den Ausdruck:
erhält man4den Ausdruck:
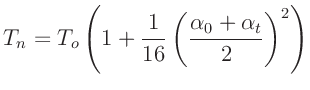 |
(5) |
Während der Messzeit von etwa 80 Sekunden (40 Perioden) nimmt die
Amplitude um weniger als 2% ab. Benutzt man statt Gleichung
5 den Ausdruck 4, bleibt der daraus resultierende
relative Fehler bis zu einer Auslenkung von 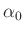 kleiner als 0.08
(entspricht etwa
kleiner als 0.08
(entspricht etwa 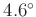 ) unter
) unter
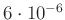 .
.
Die durch das Pendel verdrängte Luft bewirkt eine zusätzliche
Kraft. Diese Auftriebskraft ist der wirkenden Schwerkraft
entgegengerichtet und greift am Volumenmittelpunkt des Pendels an.
Für diese Kraft gilt:
Beim asymmetrischen, homogenen Pendel fallen Massen- und
Volumenmittelpunkt zusammen. Die resultierende Schwingungsgleichung
lautet damit:
und wir erhalten für die Periodendauer den Ausdruck
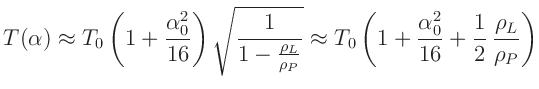 |
(6) |
Die Luftdichte 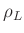 hängt vom Luftdruck
hängt vom Luftdruck 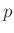 und der Temperatur
und der Temperatur 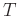 ab. Unter Annahme eines idealen Gases kann sie nach der Formel
ab. Unter Annahme eines idealen Gases kann sie nach der Formel
berechnet werden. 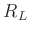 beschreibt die spezifische Gaskonstante für Luft, die
von der Luftfeuchtigkeit abhängig ist.Unter normalen Laborbedingungen, angenommen wurden
beschreibt die spezifische Gaskonstante für Luft, die
von der Luftfeuchtigkeit abhängig ist.Unter normalen Laborbedingungen, angenommen wurden
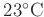 ,
,
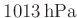 und 60%
relative Luftfeuchtigkeit, beträgt die Luftdichte
und 60%
relative Luftfeuchtigkeit, beträgt die Luftdichte
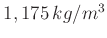 . Die im Praktikum verwendeten Pendel sind bis auf die Schneiden aus
Baustahl gefertigt, dessen Dichte je nach Kohlenstoffgehalt zwischen
. Die im Praktikum verwendeten Pendel sind bis auf die Schneiden aus
Baustahl gefertigt, dessen Dichte je nach Kohlenstoffgehalt zwischen
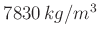 und
und
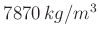 variiert.
variiert.
Bisher wurde davon ausgegangen, dass das Pendel um eine Achse
schwingt, die durch den Auflagepunkt der Schneide verläuft und durch
die Schnittlinie der beiden Seitenflächen der
prismenförmigen Schneide definiert wird. In der Praxis ist das nicht
der Fall. Die Schneide ist mehr oder weniger verrundet. Den Einfluss
des Abrollens der Schneide auf der Unterlage auf die Schwingungszeit
des Pendels hat schon von dem französischer Mathematiker Laplace
5erkannt. Sehr detailliert wurde dieser
Effekt von F.W.Bessel (1828) in den Paragraphen 25-27 und in der
Beilage IX untersucht.
Dabei geht er davon aus, dass sich die Schneidenform durch einen
Abbildung 5:
Form der Schneide
![\begin{figure}\begin{center}
\begin{picture}(87,75)
%% 0 0 494 424 ==> 174 x 1...
...cs[width=75mm]{GeometrieBesselSchneide}
\end{picture}
\end{center}\end{figure}](Timg193.png) |
Kegelschnitt beschreiben lässt, der die beiden Seitenflächen
tangiert. Der Abstand der beiden Berührungspunkte wird mit 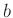 und
der Winkel zwischen den beiden Seitenflächen mit
und
der Winkel zwischen den beiden Seitenflächen mit 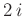 bezeichnet.
In dem fest mit der Schneide verbundenen Koordinatensystem
bezeichnet.
In dem fest mit der Schneide verbundenen Koordinatensystem
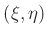 , dessen Ursprung sich im Auflagepunkt des Pendels in
Ruhelage befindet, kann die Schneidenform durch die
Scheitelpunktsgleichung des Kegelschnittes beschrieben werden.
, dessen Ursprung sich im Auflagepunkt des Pendels in
Ruhelage befindet, kann die Schneidenform durch die
Scheitelpunktsgleichung des Kegelschnittes beschrieben werden.
Dabei bedeutet 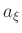 die halbe Achse in
die halbe Achse in 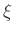 und
und 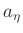 die halbe Achse in
die halbe Achse in
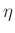 . Die von F.W.Bessel (1828) verwendete numerische
Exzentrizität
. Die von F.W.Bessel (1828) verwendete numerische
Exzentrizität
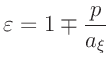 - Ellipse, + Hyperbel
- Ellipse, + Hyperbel
weicht von der heute üblichen Definition ab. Sie erlaubt auch Werte
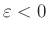 für Ellipsen
für Ellipsen
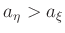 .
Damit lassen sich alle möglichen Schneidenformen über den Parameter
.
Damit lassen sich alle möglichen Schneidenformen über den Parameter
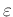 definieren. Der Größe des Formparameter
definieren. Der Größe des Formparameter
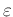 bestimmt den Wert des Faktors
bestimmt den Wert des Faktors 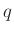 , der zur Beschreibung des Einflusses
der Schneidenform auf die gemessene Periodendauer benötigt wird.
, der zur Beschreibung des Einflusses
der Schneidenform auf die gemessene Periodendauer benötigt wird.
| |
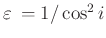 |
Winkelspitze (entartete Hyperbel) |
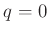 |
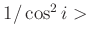 |
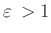 |
Hyperbel |
|
| |
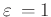 |
Parabel |
|
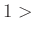 |
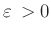 |
Ellipse mit langer Achse
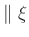 |
|
| |
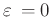 |
Kreis |
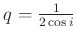 |
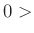 |
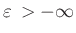 |
Ellipse mit kurzer Achse
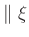 |
|
| |
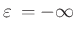 |
ebene Abstumpfung |
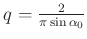 für für
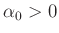 |
|
Dieser hängt außerdem von der Auslenkung 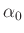 des schwingenden Pendels
ab. Für
des schwingenden Pendels
ab. Für
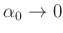 ergibt sich der Grenzwert
ergibt sich der Grenzwert
Wie die von F.W.Bessel (1828) berechneten Tabellen
6zeigen, kann
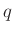 für abgestumpfte Schneiden
für abgestumpfte Schneiden
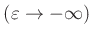 sehr
große Werte annehmen, die zu erheblichen Fehlern bei der Bestimmung
der Erdbeschleunigung führen werden. Als oberer Grenzwert kann
sehr
große Werte annehmen, die zu erheblichen Fehlern bei der Bestimmung
der Erdbeschleunigung führen werden. Als oberer Grenzwert kann
angesehen werden.
Für die Länge 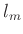 eines mathematischen Pendels, das mit der gleichen
Periodendauer wie das Schneidenpendel schwingt, hat
F.W.Bessel (1828) in der Beilage IX den Zusammenhang
eines mathematischen Pendels, das mit der gleichen
Periodendauer wie das Schneidenpendel schwingt, hat
F.W.Bessel (1828) in der Beilage IX den Zusammenhang
hergeleitet. Hierbei bedeutet 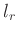 die Länge eines physikalischen
Pendels mit der gleichen Periodendauer wie das Schneidenpendel, wenn
dieses um den Auflagepunkt der Schneide schwingen würde.
die Länge eines physikalischen
Pendels mit der gleichen Periodendauer wie das Schneidenpendel, wenn
dieses um den Auflagepunkt der Schneide schwingen würde. 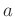 ist der
Abstand des Schwerpunktes von der Schneide. Sowohl
ist der
Abstand des Schwerpunktes von der Schneide. Sowohl 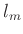 als auch
als auch 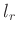 sind unbekannt. Für den Fall, dass die gemessene
Periodendauern für beide Schneiden gleich sind, gilt:
sind unbekannt. Für den Fall, dass die gemessene
Periodendauern für beide Schneiden gleich sind, gilt:
Aus diesen Gleichungen lässt sich die unbekannte Größe
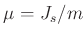 eliminieren. Unter Vernachlässigung kleiner Terme
7erhält man den Ausdruck:
eliminieren. Unter Vernachlässigung kleiner Terme
7erhält man den Ausdruck:
Der Fehler bei der Bestimmung von 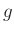 resultiert aus der
unterschiedlichen Abnutzung der Schneidenkanten. Nur für den Fall,
dass die Form beider Schneiden identisch ist (
resultiert aus der
unterschiedlichen Abnutzung der Schneidenkanten. Nur für den Fall,
dass die Form beider Schneiden identisch ist (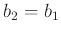 und
und
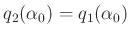 ), hebt sich der Einfluss der Schneidenform
auf und es gilt
), hebt sich der Einfluss der Schneidenform
auf und es gilt
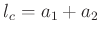 . Dies kann durch die Verwendung nur
einer festen Schneide als Auflage erreicht werden. Das Pendel ist dazu mit zwei ebenen, zueinander parallelen Flächen
auszustatten. Der Abstand dieser Schwingungsflächen bestimmt dann den
Wert von
. Dies kann durch die Verwendung nur
einer festen Schneide als Auflage erreicht werden. Das Pendel ist dazu mit zwei ebenen, zueinander parallelen Flächen
auszustatten. Der Abstand dieser Schwingungsflächen bestimmt dann den
Wert von
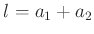 .
.
Weitestgehend eliminieren lässt sich der Einfluss der Schneidenform
auch durch Vertauschen der Schneiden (F.W.Bessel (1828)). Dazu
wird zuerst die Periodendauer
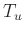 nach Gleichung 3 bestimmt. Nach Vertauschen der Schneiden
wird in der gleichen Weise
nach Gleichung 3 bestimmt. Nach Vertauschen der Schneiden
wird in der gleichen Weise 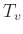 ermittelt. Aus
ermittelt. Aus
kann 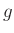 unabhängig von der Form der Schneiden bestimmt werden.
unabhängig von der Form der Schneiden bestimmt werden.
Welchen Einfluss die Schneidenform hat, kann man an der Veränderung der
Amplitudenabhängigkeit der Periodendauer erkennen. Aus dem Ausdruck für 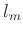 folgt unter der Annahme sehr stark abgestumpfter Schneiden
folgt unter der Annahme sehr stark abgestumpfter Schneiden
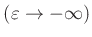 für die Amplitudenabhängigkeit der
Periodendauer
für die Amplitudenabhängigkeit der
Periodendauer
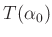 als oberer Grenzwert die Korrektur
als oberer Grenzwert die Korrektur
In Abbildung 6 (mit dem GnuPlot-Skript
Amplitudenabhaengigkeit.gnuplot
berechnet)
ist die gemessene Abhängigkeit der Periodendauer von der Amplitude
zusammen mit einem Fit nach Gleichung 4 sowie einem Fit nach Gleichung
7 dargestellt. Die Auswirkungen der Scheidenform auf
Abbildung 6:
Auswirkung der Schneidenform auf die Periodendauer
![\begin{figure}\centering
%
\includegraphics[width=93mm]{Amplitudenabhaengigkeit-Platz3Schneide2-20160504}
\end{figure}](Timg313.png) |
die Periodendauer ist hier sehr deutlich zu erkennen. Aus dem Fit
folgt bei einem Schwerpunktsabstand 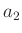 von etwa 620mm ein Wert
für b, der Breite der Abflachung der Schneide, von etwa
von etwa 620mm ein Wert
für b, der Breite der Abflachung der Schneide, von etwa 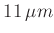 .
.
Liegt
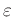 in der Nähe von 0, ist
in der Nähe von 0, ist 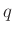 nur noch sehr wenig
oder im Falle einer zylindrischen Schneide
nur noch sehr wenig
oder im Falle einer zylindrischen Schneide
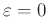 gar nicht
von der Amplitude
gar nicht
von der Amplitude 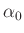 abhängig. In diesem Fall gilt
abhängig. In diesem Fall gilt 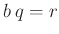 ,
wobei
,
wobei 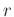 der Radius der Schneide ist. Da im allgemeinen keine
Informationen über die genaue Form der beiden Schneiden vorliegen und
man davon ausgehen muss, dass die Abstumpfung der beiden Schneiden
unterschiedlich ist, kann dieser Fehler im Nachgang nicht korrigiert
werden.
der Radius der Schneide ist. Da im allgemeinen keine
Informationen über die genaue Form der beiden Schneiden vorliegen und
man davon ausgehen muss, dass die Abstumpfung der beiden Schneiden
unterschiedlich ist, kann dieser Fehler im Nachgang nicht korrigiert
werden.
Die gemessenen Amplitudenabhängigkeiten zeigen, dass die Schneiden an
allen vier im Praktikum genutzten Reversionspendeln deutlich abgeflacht
sind. In diesem Fall ist bei den üblicherweise verwendeten
Auslenkungen von weniger als 0.5 Grad der Einfluss derunterschiedlichen Form der beiden Schneiden besonders stark
bemerkbar. Ohne Veränderungen an den Pendeln vorzunehmen, lässt sich
er sich durch die Messung bei größeren Amplituden entsprechend
Gleichung 7 verringern. Werden die Messung mit einer
Amplitude von 2.5 Grad durchgeführt, verringert sich der Einfluss der
Abstumpfung um etwa den Faktor 5.
In Folge der inneren Reibung in der aerodynamischen Grenzschicht
haftet ein kleiner Teil der angrenzenden Luftmasse an der
Pendeloberfläche. Dadurch vergrößert sich das Trägheitsmoment des
Pendels um einen kleinen unbekannten Betrag. Diesen Effekt hat schon
F.W.Bessel (1828) ausführlich untersucht. Bei einem homogenen
asymmetrischen Pendel sind die zusätzlichen Trägheitsmomente für beide
Schneiden unterschiedlich. Ihr Einfluss kann sich daher nur teilweise
kompensieren. Bei einem inhomogenen, aber in der Form symmetrischen
Pendel ergibt sich für beide Schneiden das gleiche zusätzliche
Trägheitsmoment. Bei der Methode der Schnittpunktsbestimmung
verschwindet dieses zusammen mit dem zusätzlichen Trägheitsmoment
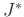 (siehe hierzu Herleitung der Gleichung 3).
(siehe hierzu Herleitung der Gleichung 3).
Bisher wurde davon ausgegangen, dass das Reversionspendel ein starrer
Körper ist. Spätestens bei der Durchführung der Schwerpunktsbestimmung
wird deutlich, dass diese Annahme nicht erfüllt ist. Wenn das
Pendel genau unter dem Schwerpunkt unterstützt wird, ist die
Durchbiegung des Pendelstabes unter dem Einfluss der Gewichtskraft
deutlich sichtbar.
Abbildung 7:
FEM-Modell des im Schwerpunkt unterstützten
Reversionspendel. Die Durchbiegung von etwa mehr als 3 mm ist um
den Faktor 10 überhöht gezeichnet.
![\begin{figure}\centering
%
\includegraphics[width=123.11mm]{FEM-Reversionspendel-mitStuetze}
\end{figure}](Timg323.png) |
Eine Simulation (Abbildung 7) mittels der finite Elemente
Methode (Programmpaket CalculiX (2016)) ergab, dass die Enden
des Pendels etwa 3.3mm tiefer liegen als der Unterstützungspunkt.
F.R.Helmert (1898) hat gezeigt, dass durch die
Elastizität des Reversionspendels systematischen zu große Werte für die
Länge des einfachen Sekundenpendels und damit zu große Werte für g
bestimmt werden. Bei dem von ihm detailliert untersuchten stark
biegsamen Meterpendel betrug die experimentell bestimmte relative
Abweichung
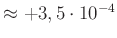 .
.
Pendel und Pendelaufhängung bilden ein Gesamtsystem. Beim Schwingen
wirkt auf die Auflageflächen eine sich periodisch ändernde Kraft, die
das Stativ zum Mitschwingen anregt.
Insgesamt ergibt sich, dass die Konstruktion der im Versuch M9
genutzten, wenigstens 45 Jahre alten Reversionspendel den
Möglichkeiten der heute zur Verfügung gestellten Zeit- und
Längenmessgeräten nicht mehr entsprechen.
Die störenden Einflüsse der umgebenden Luft können durch ein
symmetrisch geformtes, inhomogenes Pendel, wie es bereits
F.W.Bessel (1828) vorgeschlagen hat, vollständig vermieden
werden. Durch Verwendung von am Pendel angebrachten Schwingungsflächen
und nur einer festen Schneide, auf der das Pendel schwingt,
kompensiert sich weitestgehend die Auswirkung der Schneidenform auf
das Endergebnis. Wie ein solches, für Lehrzwecke verwendbares
Reversionspendel, aussehen kann wurde, von D.Candela u.a. (2001)
ausführlich beschrieben. Dabei wird auch auf eine ausreichende
Steifheit der Pendelaufhängung geachtet.
Die mit diesem Pendel erreichte
Messgenauigkeit (Abweichung vom Referenzwert des Messortes) bei der
Bestimmung von g liegt unter
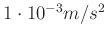 .
.
Vor Beginn der Zeitmessungen muss die Ausrichtung des Lasers an der
Lichtschranke kontrolliert werden. Das Starten und Stoppen der Uhr,
dass durch die Freigabe der Lichtschranke erfolgt, sollte in
unmittelbarer Nähe des Nulldurchganges des Pendels erfolgen.
Der Laserspot ist daher so eingestellt, dass er die Pendelstange an
der wandseitigen Seite gerade streift und
Abbildung 8:
Justage der Lichtschranke
![\begin{figure}\centering
%
\includegraphics[width=52mm]{JustageLichtschranke}
\end{figure}](Timg326.png) |
die eine Hälfte des Lichtflecks noch auf der Eintrittsblende der
Photodiode zu sehen ist. Sollte dies nicht der Fall sein, ist die
Lichtschranke mit Hilfe des Versuchsbetreuers neu einzustellen.
Danach kann mit den Messungen begonnen werden.
- Übersichtsmessung
Für die Übersichtsmessung wird das Pendel mit der Schneide 2
eingehangen. Das Laufgewicht wird so nahe wie möglich an die Schneide
2 herangeschoben und mit seiner Oberkante auf der nächsten Ringmarke
ausgerichtet und fixiert. Es wird die Zeit für 4 Perioden für
Schneide 2 und nach Umdrehen des Pendel für Schneide 1 mit einer
Amplitude von ca. 45mm gemessen. Damit die richtige Seite der
Pendelstange die Zeitmessung bestimmt, muss die Uhr immer in der Nähe des
wandseitigen Umkehrpunktes gestartet werden. Nach der erfolgten
Messung der beiden Zeiten wird das Pendel wieder mit der Schneide 2
aufgehängt und danach das Laufgewicht in Richtung Schneide 1 um eine
Ringmarke verschoben. Danach werden die Zeiten für beide Schneiden erneut
gemessen. Dieser Ablauf wird solange wiederholt, bis sich das
Vorzeichen der Differenz 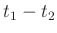 ändert. Der gesuchte Schnittpunkt
der beide Kurven muss zwischen der vorhergehenden und der momentanen
Position des Laufgewichtes liegen. An dieser Stelle wird die
Übersichtsmessung beendet. Die genaue Lage des Schnittpunktes kann
mit der Gleichung
ändert. Der gesuchte Schnittpunkt
der beide Kurven muss zwischen der vorhergehenden und der momentanen
Position des Laufgewichtes liegen. An dieser Stelle wird die
Übersichtsmessung beendet. Die genaue Lage des Schnittpunktes kann
mit der Gleichung
berechnete werden. Dabei bezeichnet der erste Index die Position des
Laufgewichtes. Der zweite Index steht für die jeweilige Schneide. Da
der Ringmarkenabstand mit 20mm bekannt ist, kann das Laufgewicht
auf etwa
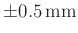 genau fixiert werden. Diese Position
wird im weiteren Verlauf des Versuchs nicht mehr verändert. Die für
beide Schneiden gemessenen Zeiten (4 Perioden) sollten sich um
weniger als 20ms unterscheiden. Ist das nicht der Fall sollte die
Berechnung von
genau fixiert werden. Diese Position
wird im weiteren Verlauf des Versuchs nicht mehr verändert. Die für
beide Schneiden gemessenen Zeiten (4 Perioden) sollten sich um
weniger als 20ms unterscheiden. Ist das nicht der Fall sollte die
Berechnung von 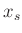 und die Positionierung des Laufgewichtes
nochmals überprüft werden.
und die Positionierung des Laufgewichtes
nochmals überprüft werden.
- Präzisionsmessung
Für die Präzisionsmessung wird die Zeit für 40 Perioden bei einer
Auslenkung von 45mm für beiden Schneiden gemessen. Diese Messung
ist jeweils 10 mal zu wiederholen. Damit alle zufälligen Störgrößen erfasst
werden, ist nach jeder Messung das Pendel umzudrehen, sodass die
Zeiten für die Schneiden 1 und 2 wechselweise gemessen werden. Aus
den Mittelwerten kann mit der Gleichung
die Zeit für 40 Schwingungen
am Schnittpunkt berechnet werden. Durch Anwendung des
Fehlerfortpflanzungsgesetzes erhält man aus den Vertrauensbereichen
den zufälligen Fehler der so bestimmten Schwingungszeit am
Schnittpunkt. Da der systematische Restfehler der verwendeten Uhr
sich auf alle Zeitmessungen in gleicher Weise auswirkt, ist dieser
nach Größtfehlerabschätzung mit dem bestimmten zufälligen Fehler zu
verknüpfen. Aus der Zeit für 40 Schwingungen und deren Fehler ergibt
sich die Periodendauer und deren Fehler.
- Schneidenabstand und Schwerpunkt
Der Schneidenabstand wird mit Hilfe eines Anbaumessschiebers
gemessen. Um zufällige Störeinflüsse zu berücksichtigen ist diese
Messung 10 mal zu wiederholen und daraus Mittelwert und
Vertrauensbereich zu bestimmen. Alle notwendigen Angaben sind am
Messplatz angegeben.
Abbildung 9:
Bestimmung des Schwerpunktes
![\begin{figure}\centering
%
\includegraphics[width=120.65mm]{Schwerpunktbestimmung}
\end{figure}](Timg337.png) |
Der Abstand des Schwerpunktes von der Schneide 1 wird durch
Ausbalancieren des Pendels auf einem vertikalen Stahlblech
bestimmt. Die Dicke diese Bleches beträgt 1mm. Der Abstand
zwischen der Schneide 1 und der Mitte des Stützbleches wird mit einem
Stahllineal gemessen. Zur Abschätzung der Messgenauigkeit können
hier auch mehrere Wiederholungen durchgeführt werden. Diese sind
jedoch nur dann aussagekräftig, wenn das Pendel jedesmal neu
ausbalanciert wird.
- Amplitudenabhängigkeit
Für eine der beiden Schneiden ist die Amplitudenabhängigkeit der
Zeit für 40 Schwingungen aufzunehmen.
Die Vorwahleinstellung ist entsprechend der jeweiligen Amplitude
vorzunehmen. Bei Auslenkungen kleiner als etwa 16mm (Durchmesser der
Pendelstange) wird die Lichtschranke nur einmal pro Schwingung
freigegeben. In diesem Fall ist die Vorwahl auf die halbe
Periodenanzahl 20 einzustellen. Es sollten jeweils wenigstens
11 verschiedene Auslenkungen zwischen 5 und 100 mm genutzt
werden.
Bei der Auswertung unter Anwendung der Gleichungen
und
sollte zusätzlich das Ergebnisse der Präzisionsmessung als weiterer
Datenpunkt einbezogen werden. Unbekannt und daher Fitparameter ist
im ersten Fall der Wert von 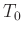 . Bei der zweiten Abhängigkeit ist
der Wert der Schneidenbreite
. Bei der zweiten Abhängigkeit ist
der Wert der Schneidenbreite 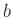 ein weiterer Fitparameter für die
Anpassung der Funktion an die Messpunkte. Als Startwert kann von
ein weiterer Fitparameter für die
Anpassung der Funktion an die Messpunkte. Als Startwert kann von
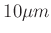 ausgegangen werden. Der Abstand
ausgegangen werden. Der Abstand 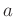 der betrachteten
Schneide zum Schwerpunkt ist durch die zuvor durchgeführten
Messungen von
der betrachteten
Schneide zum Schwerpunkt ist durch die zuvor durchgeführten
Messungen von 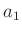 und
und 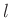 bekannt.
bekannt.
In der Darstellung von
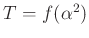 wird der Unterschied
zwischen beiden verschiedenen Funktionen am deutlichsten sichtbar.
wird der Unterschied
zwischen beiden verschiedenen Funktionen am deutlichsten sichtbar.
-
Physikalisches Grundpraktikum: Mechanik und Thermodynamik
Versuch M9: Reversionspendel, Seiten 51...54
Mathematisch-Naturwissenschaftliche Fakultät der HUB
Institut für Physik (2012)
- http://gpr.physik.hu-berlin.de/Skripten/Mechanik und Thermodynamik/PDFDateien/Mechanik und Thermodynamik.pdf
abgerufen am 6.3.2016 19:03 Uhr
-
J.G.F.Bohnenberger
Astronomie
Drittes Buch, Kapitel II, §266, Seiten 447...449 und Tafel VI, Zeichnung 102
Tübingen (1811)
-
H.Kater
An Account of Experiments for Determining the Length of the Pendulum
Vibrating Seconds in the Latitude of London
Philosophical Transactions of the Royal Society of London
Vol.108, pages 33...102 (1818)
-
F. W. Bessel
Untersuchungen über die Länge des einfachen Secundenpendels
Abhandlungen der Königlichen Akademie der Wissenschaften zu Berlin
(1828)
-
J.G.F.Bohnenberger
Ueber die Bestimmung der Länge des einfachen Secundenpendels
Naturwissenschaftliche Abhandlungen,
Herausgegeben von einer Gesellschaft in Würtemberg
Erster Band, Drittes Heft, Seiten 1-34 und Tafel I
Tübingen (1827)
-
F. W. Bessel
Construction eines symmetrisch geformten Pendels mit reciproken Axen
Astronomische Nachrichten
Band30, Heft1, (No. 697), Seite 1...6 (1850)
-
F.R.Helmert
Beiträge zur Theorie des Reversionspendels
Veröffentlichung des Königl. Preuszischen Geodätischen Instituts
und Centralbureaus der Internationalen Erdmessung
Potsdam (1898)
-
J.H.Poynting and J.J.Thomson
A Text-Book of Physics, Properties of Matter
Chapter II. The Acceleration of gravity, pages 7...20
London (1902)
-
F.Kühnen, Ph.Furtwängler
Bestimmung der absoluten Grösze der Schwerkraft zu Potsdam
mit Reversionspendeln
Veröffentlichung des Königl. Preuszischen Geodätischen Instituts
Neue Folge No. 27, Berlin (1906)
-
R.M. Dreizler und C.S. Lüdde
Theoretische Physik Band 1: Theoretische Mechanik
Springer 2008 ISBN 978-3-540-70557-4
- http://www.springer.com/de/book/9783540705574
abgefufen am 2.2.2018 17:39 Uhr
-
A.H.Cook
The Absolute Determination of the Acceleration Due to Gravity
Metrologia Vol.1, pages84...114
(1965)
-
D.Candela, K.M.Martini, R.V.Krotkov und K.H.Langley
Bessel's improved Kater pendulum in the teaching lab
Am.J.Phys. Vol69, No.6, pages 714...720
(2001)
-
Joachim Höpfner
Absolute Bestimmung der Schwere mit Reversionspendeln in Potsdam
1898-1904 und 1968-1969
Deutschen Gesellschaft für Chronometrie, Jahresschrift
Band51, Seiten101...114 (2012)
-
Guido Dhondt, Klaus Wittig
CalculiX CrunchiX (ccx) und CalculiX GraphiX 2.11 (cgx)
Version 2.11 (2016)
- http://www.calculix.de/
abgerufen am 4.10.2016 10:04 Uhr
Fußnoten
- ...
einzustellen1
- Nach F.Kühnen, Ph.Furtwängler (1906), Seite X wird diese Erkenntnis Bohnenberger
zugeschrieben. Der dort angegebene Quelle
(J.G.F.Bohnenberger (1811)) kann diese Aussage jedoch nicht
entnommen werden. Auch in J.G.F.Bohnenberger (1827) findet sich
kein Hinweis darauf. F.W.Bessel (1828) (Seite 97)
geht bei seinen Betrachtungen davon aus, das ein bewegliches Gewicht
für ein Pendel mit reziproken Achsen nicht erforderlich ist, sondern
es ausreicht, wenn die Schwingungszeiten um beide Schneiden nahezu
gleich gemacht werden.
- ... Gleichung2
- Diese Gleichung findet man ohne Herleitung oder Quellenangabe bei
F.Kühnen, Ph.Furtwängler (1906) auf Seite X und bei F.R.Helmert (1898)
auf Seite 8 (Gleichung 24) als Ausgangspunkt weiterer
Überlegungen. Nach J.H.Poynting and J.J.Thomson (1902) (Seite 15) geht
dieser Ausdruck auf F.W.Bessel (1828) zurück, auch wenn er sich
dort nicht direkt findet, sondern nur die Überlegungen, die zur
Herleitung notwendig sind, angegeben werden.
- ...
herleiten3
- Für den Fall das die Periodendauern für beide Schneiden
gleich sind, gilt
Daraus folgt für das Schwerpunktsträgheitsmoment 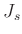 :
:
Sind die beiden Periodendauern 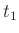 und
und 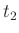 nicht exakt gleich,
kann man für
nicht exakt gleich,
kann man für 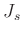
schreiben, wobei das zusätzliche Trägheitsmoment 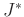 bei kleiner
Differenz der Periodendauern ebenfalls sehr klein ist.
Aus der Lösung der Schwingungsgleichung für das physikalische Pendel
bei kleiner
Differenz der Periodendauern ebenfalls sehr klein ist.
Aus der Lösung der Schwingungsgleichung für das physikalische Pendel
folgt mit
die Beziehung
und daraus:
Analog gilt für die 2. Schneide:
Damit lässt sich die unbekannte Größe 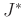 aus den Gleichungen
eliminieren.
aus den Gleichungen
eliminieren.
und erhält den Ausdruck:
Schreibt man für den Mittelwert 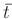 und die Differenz
und die Differenz 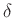 :
:
und ersetzt damit die Größen 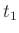 und
und 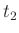 durch
durch
so erhält man:
mit
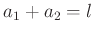 ergibt sich daraus der exakte Ausdruck für die
Periodendauer des Reversionspendels:
ergibt sich daraus der exakte Ausdruck für die
Periodendauer des Reversionspendels:
Diese Herleitung findet man in sehr kompakter Form in
A.H.Cook (1965) auf Seite 89. Geht man wieder auf die
ursprünglichen Größen 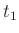 und
und 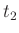 zurück, so erhält man den von
F.W.Bessel (1828) angegebenen Ausdruck:
zurück, so erhält man den von
F.W.Bessel (1828) angegebenen Ausdruck:
Der Ausdruck 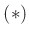 fährt auch direkt auf die Gleichung 2:
fährt auch direkt auf die Gleichung 2:
Beide Gleichung werden auch in J.H.Poynting and J.J.Thomson (1902) auf Seite 15
unter Verweis auf F.W.Bessel (1828) hergeleitet.
- ... man4
-
Die folgende Herleitung ist zum Teil A.H.Cook (1965) (Seite 89)
entnommen. Aus der Zeitabhängigkeit der Periodendauer folgt für die
Kreisfrequenz:
Der Phasenwinkel 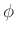 nach der Zeit
nach der Zeit 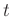 ergibt sich zu:
ergibt sich zu:
Wird dieser Phasenwinkel einem ganzzahligen Vielfachen von 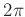 gleichgesetzt,
gleichgesetzt,
so erhält man für die über n Perioden gemittelte Periodendauer 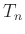
da
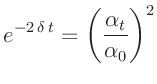 und
und 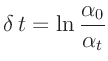
gilt, ergibt sich
Abweichend von A.H.Cook (1965) (Seite 89) wird
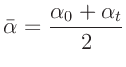 und
und 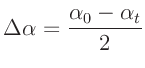
und somit
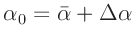 und
und 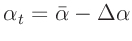
gesetzt. Damit ergibt sich
Durch Anwendung der Reihenentwicklung
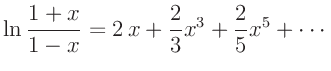 mit
mit 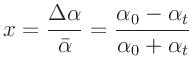
und Abbruch vor dem Term dritter Ordnung ergibt sich
und damit
A.H.Cook (1965) (Seite 89) verwendet für
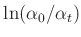 die Reihenentwicklung
die Reihenentwicklung
und bricht diese vor dem Term zweiter Ordnung ab. Damit wird
woraus die durch den früheren Abbruch der Reihenentwicklung ungenauere Abschätzung
folgt.
F.Kühnen, Ph.Furtwängler (1906) nutzen die Amplitude 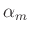 in der Mitte
der Beobachtungszeit
in der Mitte
der Beobachtungszeit 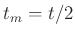 zur Berückichtigung der Dämpfung bei der
Amplitudenreduktion. Aus der auf Seite 35 angegeben Gleichung 7
zur Berückichtigung der Dämpfung bei der
Amplitudenreduktion. Aus der auf Seite 35 angegeben Gleichung 7
folgt mit
sofort der Ausdruck 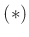 . Die Reihenentwicklung der Exponentialfunktionen des Terms
. Die Reihenentwicklung der Exponentialfunktionen des Terms
und Abbruch vor der fünften Ordnung führt auf die von
F.Kühnen, Ph.Furtwängler (1906) angegebene Reduktionsformel
- ... Laplace5
- Im Anhang von H.Kater (1818) ist eine Zusammenfassung der
Argumentation von Laplace enthalten.
- ... Tabellen6
- Die folgende Tabelle ist F.W.Bessel (1828) Seite 71/72 entnommen.
Winkel
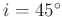 |
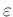 |
Kegelschnitt |
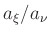 |
Werte von
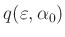 |
| |
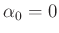 |
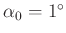 |
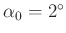 |
| + 2 |
Hyperbel |
|
0.00 |
0.00 |
0.00 |
| + 1 |
Parabel |
|
0.50 |
0.50 |
0.50 |
| 0 |
Kreis |
1: 1 |
0.71 |
0.71 |
0.71 |
| - 10 |
Ellipse |
1: 3.32 |
1.73 |
1.73 |
1.72 |
| - 100 |
|
1: 10.05 |
5.05 |
4.99 |
4.84 |
| - 1000 |
|
1: 31.64 |
15.83 |
14.30 |
11.58 |
| - 10000 |
|
1: 100.00 |
50.00 |
28.28 |
16.68 |
| -100000 |
|
1: 316.23 |
158.11 |
34.94 |
18.00 |
- 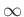 |
Ebene |
1: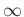 |
 |
36.48 |
18.24 |
Winkel
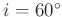 |
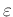 |
Kegelschnitt |
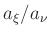 |
Werte von
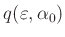 |
| |
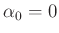 |
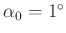 |
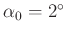 |
| + 2 |
Hyperbel |
|
0.00 |
0.00 |
0.00 |
| + 1 |
Parabel |
|
0.87 |
0.87 |
0.87 |
| 0 |
Kreis |
1: 1 |
1.00 |
1.00 |
1.00 |
| - 10 |
Ellipse |
1: 3.32 |
1.87 |
1.87 |
1.86 |
| - 100 |
|
1: 10.05 |
5.10 |
5.04 |
4.88 |
| - 1000 |
|
1: 31.64 |
15.84 |
14.32 |
11.59 |
| - 10000 |
|
1: 100.00 |
50.01 |
28.38 |
16.68 |
| -100000 |
|
1: 316.23 |
158.12 |
34.94 |
18.00 |
-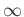 |
Ebene |
1: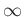 |
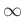 |
36.48 |
18.24 |
Der Winkel der im Praktikum genutzten Schneiden beträgt
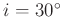 .
.
- ... Terme7
- Aus dem Umstellen beider Gleichungen nach
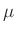 folgt:
folgt:
Damit erhält man für 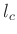
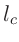 |
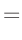 |
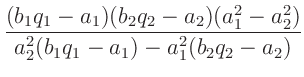 |
|
| |
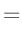 |
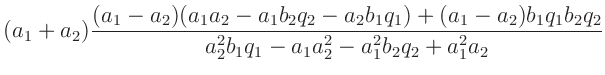 |
|
| |
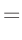 |
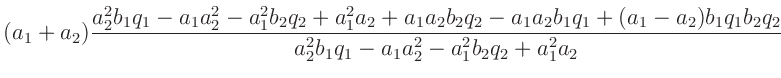 |
|
| |
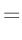 |
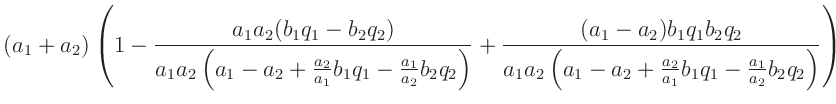 |
|
| |
|
nach Vernachlässigung des kleinen Terms 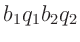 |
|
| |
|
und der kleinen Terme in 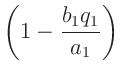 und und 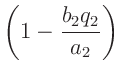 |
|
| |
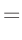 |
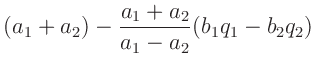 |
|
für den Fall, dass
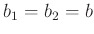 und
und
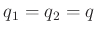 gilt, geht nur
noch der von
gilt, geht nur
noch der von 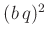 abhängige Term ein, der verschwindend gering ist.
abhängige Term ein, der verschwindend gering ist.
Peter Schaefer
2018-05-04
![]() . Der aus zehnmaliger
Wiederholung der Messung bestimmte zufällige Fehler, der
Vertrauensbereich des ermittelten Mittelwertes, beträgt meist weniger
als
. Der aus zehnmaliger
Wiederholung der Messung bestimmte zufällige Fehler, der
Vertrauensbereich des ermittelten Mittelwertes, beträgt meist weniger
als
![]() . Der daraus resultierende relative
Gesamtfehler
. Der daraus resultierende relative
Gesamtfehler ![]() der Längenmessung liegt bei einem
Schneidenabstand des Reversionspendels von
der Längenmessung liegt bei einem
Schneidenabstand des Reversionspendels von
![]() unter
unter
![]() . Dies wird auch durch die Standardabweichung der von
den Studenten in den vergangenen Jahren an den einzelnen Messplätzen
ermittelten Werte für den Schneidenabstand untermauert, die unter
. Dies wird auch durch die Standardabweichung der von
den Studenten in den vergangenen Jahren an den einzelnen Messplätzen
ermittelten Werte für den Schneidenabstand untermauert, die unter
![]() liegt.
liegt.
![]() .
Für die Bestimmung von g wird die Zeitdauer von 40 Schwingungen,
.
Für die Bestimmung von g wird die Zeitdauer von 40 Schwingungen,
![]() , mit zehnmaliger Wiederholung gemessen.
Für jede Wiederholung wird das Pendel neu ausgelenkt.
Die daraus Standardabweichung ist kleiner als
, mit zehnmaliger Wiederholung gemessen.
Für jede Wiederholung wird das Pendel neu ausgelenkt.
Die daraus Standardabweichung ist kleiner als
![]() .
Daraus resultiert ein relativer Fehler der Zeitmessung
.
Daraus resultiert ein relativer Fehler der Zeitmessung ![]() von
von
![]() .
.
![]() , das heißt mit
einem absoluten Fehler von besser als
, das heißt mit
einem absoluten Fehler von besser als
![]() ms
ms![]() bestimmbar sein. Die Ergebnisse
der letzten Jahre zeigen, dass diese Genauigkeit in den meisten Fällen
auch erreicht wird. Allerdings liegen die bestimmten Werte von g
systematisch, zum Teil um das Mehrfache des Fehlerintervalls, über dem
Referenzwert der Physikalisch-Technischen Bundesanstalt für Berlin
Adlershof. Es werden mit hoher Genauigkeit falsche Werte
bestimmt, ohne dass die Ursache für diese Abweichungen bekannt ist.
bestimmbar sein. Die Ergebnisse
der letzten Jahre zeigen, dass diese Genauigkeit in den meisten Fällen
auch erreicht wird. Allerdings liegen die bestimmten Werte von g
systematisch, zum Teil um das Mehrfache des Fehlerintervalls, über dem
Referenzwert der Physikalisch-Technischen Bundesanstalt für Berlin
Adlershof. Es werden mit hoher Genauigkeit falsche Werte
bestimmt, ohne dass die Ursache für diese Abweichungen bekannt ist.
![]() , der Abstand des
Schwerpunktes von der Schneide 1 mit
, der Abstand des
Schwerpunktes von der Schneide 1 mit ![]() und der Abstand des
Schwerpunktes von der Schneide 2 mit
und der Abstand des
Schwerpunktes von der Schneide 2 mit ![]() bezeichnet. Damit gilt
bezeichnet. Damit gilt
![]() .
.
![\begin{figure}\centering
%
\includegraphics[width=93mm]{TversusX}
\end{figure}](Timg24.png)
![\begin{figure}\centering
%
\includegraphics[width=93mm]{JversusX}
\end{figure}](Timg25.png)
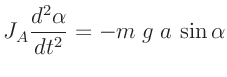
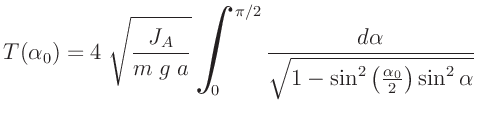
![$\displaystyle T_0\sum_{m=0}^\infty\left[\frac{(2\;m)!}{(2^m\;m!)^2}\right]^2\;\sin^{2m}\left(\frac{\alpha_0}{2}\right)$](img101.png)
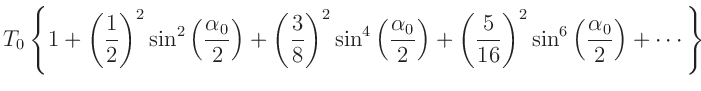
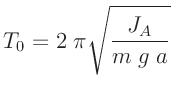
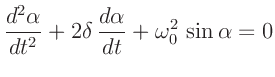 mit
mit 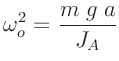
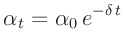
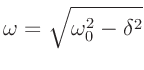
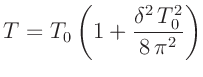
![]() .
.
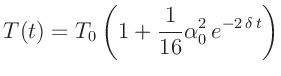
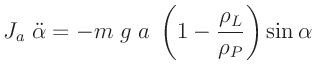
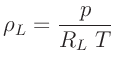
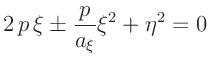 + Ellipse, - Hyperbel
+ Ellipse, - Hyperbel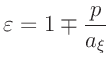 - Ellipse, + Hyperbel
- Ellipse, + Hyperbel
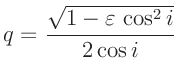
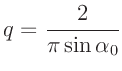
![]() eines mathematischen Pendels, das mit der gleichen
Periodendauer wie das Schneidenpendel schwingt, hat
F.W.Bessel (1828) in der Beilage IX den Zusammenhang
eines mathematischen Pendels, das mit der gleichen
Periodendauer wie das Schneidenpendel schwingt, hat
F.W.Bessel (1828) in der Beilage IX den Zusammenhang
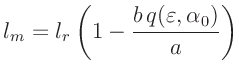
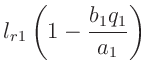 mit
mit 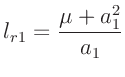
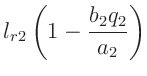 mit
mit 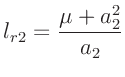
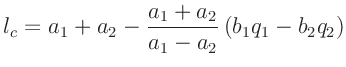
![]() nach Gleichung 3 bestimmt. Nach Vertauschen der Schneiden
wird in der gleichen Weise
nach Gleichung 3 bestimmt. Nach Vertauschen der Schneiden
wird in der gleichen Weise ![]() ermittelt. Aus
ermittelt. Aus
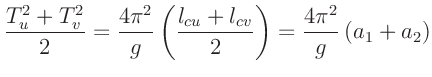
![]() folgt unter der Annahme sehr stark abgestumpfter Schneiden
folgt unter der Annahme sehr stark abgestumpfter Schneiden
![]() für die Amplitudenabhängigkeit der
Periodendauer
für die Amplitudenabhängigkeit der
Periodendauer
![]() als oberer Grenzwert die Korrektur
als oberer Grenzwert die Korrektur
![]() in der Nähe von 0, ist
in der Nähe von 0, ist ![]() nur noch sehr wenig
oder im Falle einer zylindrischen Schneide
nur noch sehr wenig
oder im Falle einer zylindrischen Schneide
![]() gar nicht
von der Amplitude
gar nicht
von der Amplitude ![]() abhängig. In diesem Fall gilt
abhängig. In diesem Fall gilt ![]() ,
wobei
,
wobei ![]() der Radius der Schneide ist. Da im allgemeinen keine
Informationen über die genaue Form der beiden Schneiden vorliegen und
man davon ausgehen muss, dass die Abstumpfung der beiden Schneiden
unterschiedlich ist, kann dieser Fehler im Nachgang nicht korrigiert
werden.
der Radius der Schneide ist. Da im allgemeinen keine
Informationen über die genaue Form der beiden Schneiden vorliegen und
man davon ausgehen muss, dass die Abstumpfung der beiden Schneiden
unterschiedlich ist, kann dieser Fehler im Nachgang nicht korrigiert
werden.
![\begin{figure}\centering
%
\includegraphics[width=123.11mm]{FEM-Reversionspendel-mitStuetze}
\end{figure}](Timg323.png)
![]() .
.
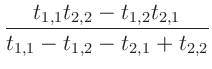
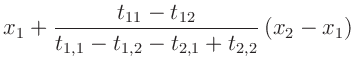
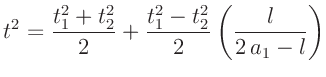
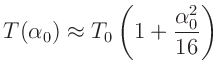
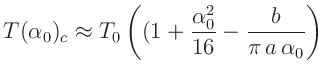
![]() wird der Unterschied
zwischen beiden verschiedenen Funktionen am deutlichsten sichtbar.
wird der Unterschied
zwischen beiden verschiedenen Funktionen am deutlichsten sichtbar.
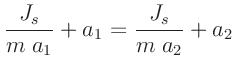
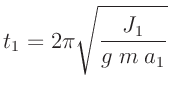
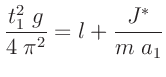
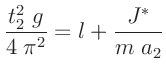
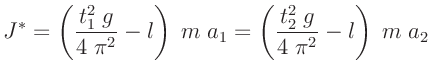
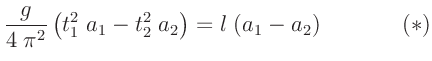
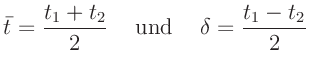
![$\displaystyle \frac{g}{4\;\pi^2}\left[(\bar{t}^2+2\;\bar{t}\;\delta + \delta^2)\;a1-(\bar{t}^2-2\;\bar{t}\;\delta+\delta^2)\;a2\right]$](img86.png)
![$\displaystyle \frac{g}{4\;\pi^2}\left[(\bar{t}^2+\delta^2)\;(a_1-a_2)+2\;\bar{t}\delta(a_1+a_2)\right]$](img88.png)
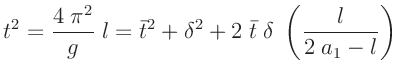
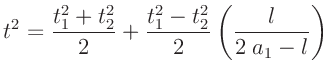
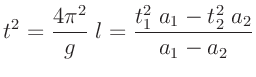
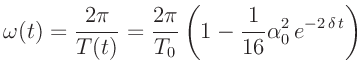
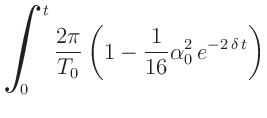
![$\displaystyle \frac{2 \pi}{T_0}\left[t-\frac{\alpha_0^2}{32\,\delta}\left(1-e^{-2\,\delta\,t}\right)\right]$](img132.png)
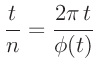
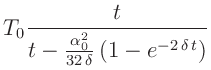
![$\displaystyle T_0 \left[1+\frac{\alpha_0^2}{32\,\delta\,t}\left(1-e^{-2\,\delta\,t}\right)\right]$](img142.png)
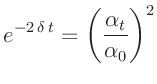 und
und 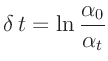
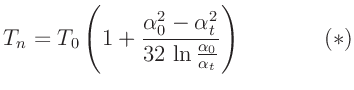
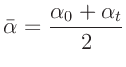 und
und 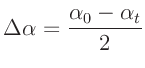
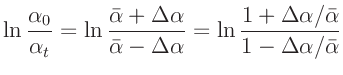
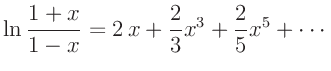 mit
mit 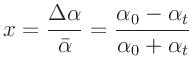
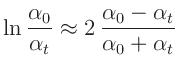
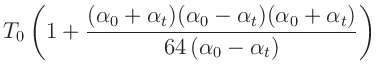
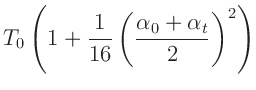
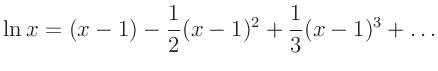
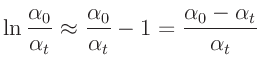
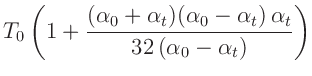
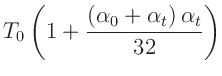
![]() in der Mitte
der Beobachtungszeit
in der Mitte
der Beobachtungszeit ![]() zur Berückichtigung der Dämpfung bei der
Amplitudenreduktion. Aus der auf Seite 35 angegeben Gleichung 7
zur Berückichtigung der Dämpfung bei der
Amplitudenreduktion. Aus der auf Seite 35 angegeben Gleichung 7
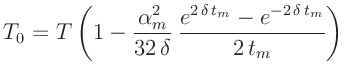
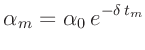 und.
und. 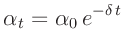 bzw.
bzw. 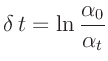
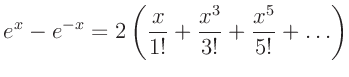
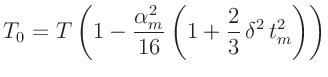
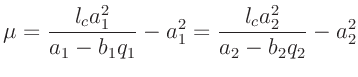
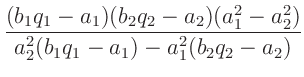
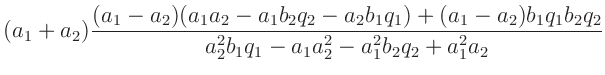
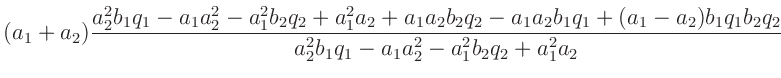
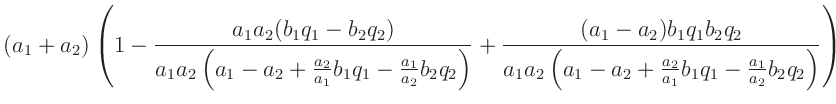
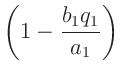 und
und