Nächste Seite: Das allgemeine lineare Modell Aufwärts: Rechnet QtiPlot falsch ? Vorherige Seite: Rechnet QtiPlot falsch ?
Bei der Durchsicht der von den Studenten im Physikalischen Grundpraktikum angefertigten Protokolle fällt auf, dass die dort mit der Methode der linearen Regression erhaltenen Ergebnisse zum Teil erheblich von den mit Mathematica (2014) berechneten Kontrollwerten abweichen.
Das Problem soll an einem einfachen Beispiel aus dem Einführungskurs
verdeutlicht werden. Beim Versuch F4 (siehe hierzu:
Einführungspraktikum (2007) Seite 9...11) wird eine Feder schrittweise
mit Massestücken von ca. 50 g belastet. Die Position ![]() einer an der
Feder befestigten Marke wird mit Hilfe einer Spiegelskala gemessen (erste
Messreihe). Nach Erreichen der Höchstbelastung mit 8 Massestücken wird die
Feder wieder schrittweise entlastet und dabei die Position der Marke erneut
abgelesen (zweite Messreihe). Die Unsicherheit der so bestimmten
Positionen
einer an der
Feder befestigten Marke wird mit Hilfe einer Spiegelskala gemessen (erste
Messreihe). Nach Erreichen der Höchstbelastung mit 8 Massestücken wird die
Feder wieder schrittweise entlastet und dabei die Position der Marke erneut
abgelesen (zweite Messreihe). Die Unsicherheit der so bestimmten
Positionen ![]() wird sowohl durch den systematischen Restfehler der
verwendeten Spiegelskala als auch durch Fehler beim Ablesen von der
Spiegelskala bestimmt. Der Mittelwert der Massen
wird sowohl durch den systematischen Restfehler der
verwendeten Spiegelskala als auch durch Fehler beim Ablesen von der
Spiegelskala bestimmt. Der Mittelwert der Massen
![]() aller
im Versuch verwendeten Massestücke beträgt 50.22g bei einer
Standardabweichung von 0,36g. Auch dieser Wert beeinflusst die
Streuung der gemessenen Positionen.
aller
im Versuch verwendeten Massestücke beträgt 50.22g bei einer
Standardabweichung von 0,36g. Auch dieser Wert beeinflusst die
Streuung der gemessenen Positionen.
Aus dem Anstieg der Geraden
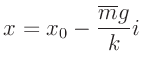 |
(1) |
Tabelle 1: Beispiel einer Messdatenreihe des Versuchs F4 |
Da mit dem systematischen Restfehler der verwendeten Spiegelskala
![]() (Einführungspraktikum (2007) Seite 11) eine
Abschätzung des Fehlers der Position
(Einführungspraktikum (2007) Seite 11) eine
Abschätzung des Fehlers der Position ![]() vorliegt und dieser für die
einzelnen Messpunkte unterschiedlich ist, erscheint die Anwendung der
gewichteten linearen Regression sinnvoll. Diese Methode wird z.B.
von Nollau (1975) (Seiten 152...156) oder Fahrmeir (2009)
(Seiten 124...127) ausführlich beschrieben. Bei der instrumentellen
Gewichtung werden die Größen
vorliegt und dieser für die
einzelnen Messpunkte unterschiedlich ist, erscheint die Anwendung der
gewichteten linearen Regression sinnvoll. Diese Methode wird z.B.
von Nollau (1975) (Seiten 152...156) oder Fahrmeir (2009)
(Seiten 124...127) ausführlich beschrieben. Bei der instrumentellen
Gewichtung werden die Größen
![]() als Gewichte
verwendet.
als Gewichte
verwendet. ![]() ist dabei die Varianz, das Fehlerquadrat, der
jeweiligen Position
ist dabei die Varianz, das Fehlerquadrat, der
jeweiligen Position ![]() und
und ![]() eine frei wählbare Konstante, die
oftmals gleich 1 gesetzt wird.
eine frei wählbare Konstante, die
oftmals gleich 1 gesetzt wird.
Die Ergebnisse der obigen Messreihe mit der Methode der instrumentell
gewichteten linearen Regression mit den beiden zuvor schon genutzten
Auswerteprogrammen sind ebenfalls in der Tabelle 2
aufgelistet. Zusätzlich erfolgte eine Auswertung der
Daten mit den Formeln aus Nollau (1975) und
Fahrmeir (2009) sowie mit den im Einführungsskript (2007) auf
Seite 41,42 angegebenen Gleichungen 43 und 45. Letztere lässt sich aus
der von Wolff (2014) auf den Seite 117/118 hergeleiteten
Gleichung 9.20 für
![]() ableiten.
ableiten.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ein erster Hinweis darauf findet sich bei James (2006) auf Seite 3.
The Bayesian approach is closer to everyday reasoning, where probability is interpreted as a degree of belief that something will happen, or that a parameter will have a given value.
The frequentist approach is closer to scientific reasoning, where probability means the relative frequency of something happening. This make it more objective, since it can be determined independently of the observer, but restricts its application to repeatable phenomina. ``
Liegt die Ursache für die unterschiedlichen Formeln und Ergebnisse in den Unterschieden zwischen diesen beiden Richtungen begründet? Dazu sollen die jeweiligen Aussagen näher betrachtet werden, wobei eine Beschränkung auf das allgemeine linear Modell erfolgt. Zu den Grundlagen, zu Herleitungen und Beweisen sowie zu weiterführenden Fragen sei auf die angegebene Literatur verwiesen.
schaefer 2017-12-09