Den Ausgangspunkt bildet eine Reihe von 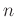 Messwerten,
Messwerten,
die in Abhängigkeit von 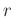 nicht stochastischen Einflussgrößen
erhalten wurden. Die
nicht stochastischen Einflussgrößen
erhalten wurden. Die 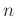 Vektoren
Vektoren
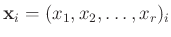 müssen dabei nicht
alle unterschiedliche Werte besitzen. Die Abhängigkeit der Messwerte
von den Einflussgrößen kann über
müssen dabei nicht
alle unterschiedliche Werte besitzen. Die Abhängigkeit der Messwerte
von den Einflussgrößen kann über
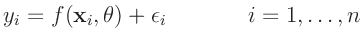 |
(2) |
beschrieben werden. Die Spaltenvektoren
enthalten die 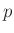 unbekannten Parameter des Modells beziehungsweise
eine unabhängige Zufallsgröße, die die Abweichungen der Messwerte
unbekannten Parameter des Modells beziehungsweise
eine unabhängige Zufallsgröße, die die Abweichungen der Messwerte
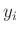 von den aus dem Modell berechneten Werten beschreibt. Für den
Erwartungswert
von den aus dem Modell berechneten Werten beschreibt. Für den
Erwartungswert
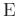 und die Varianz
und die Varianz
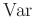 dieser Größe soll gelten:
dieser Größe soll gelten:
![$\displaystyle \bm{\mathrm{E}}[\bm{\epsilon}] = 0$](img46.png) und und![$\displaystyle \hspace{5mm} \bm{\mathrm{Var}}[\bm{\epsilon}] = \sigma^2$](img47.png) |
(3) |
wobei 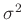 im allgemeinen unbekannt ist. Weitere Annahmen über
die Verteilung der
im allgemeinen unbekannt ist. Weitere Annahmen über
die Verteilung der
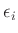 , insbesondere die Voraussetzung einer
Normalverteilung, sind an dieser Stelle nicht notwendig.1Damit gilt für den Erwartungswert2vom
, insbesondere die Voraussetzung einer
Normalverteilung, sind an dieser Stelle nicht notwendig.1Damit gilt für den Erwartungswert2vom 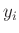 :
:
![$\displaystyle \bm{\mathrm{E}}[y_i] = f(\bm{x}_i,\bm{\theta}) \hspace{15mm} i = 1,\ldots,n$](img55.png) |
(4) |
Wenn sich die Funktion
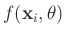 als Linearkombination von
als Linearkombination von 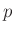 beliebigen, nicht notwendigerweise linearen Funktionen
beliebigen, nicht notwendigerweise linearen Funktionen
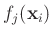 darstellen lässt, kann man dafür schreiben:
darstellen lässt, kann man dafür schreiben:
![$\displaystyle \bm{\mathrm{E}}[y_i] =\sum_{j=1}^p \theta_j f_j(\bm{x}_i) \hspace{15mm} i = 1,\ldots,n$](img59.png) |
(5) |
In diesem Fall liegt ein in den Parametern
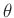 lineares Modell
vor. Aus diesem lassen sich verschiedene Spezialfälle
ableiten. Wenn zum Beispiel die Messwerte nur von einer Einflussgröße
lineares Modell
vor. Aus diesem lassen sich verschiedene Spezialfälle
ableiten. Wenn zum Beispiel die Messwerte nur von einer Einflussgröße
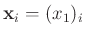 linear abhängen, kann
linear abhängen, kann
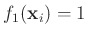 sowie
sowie
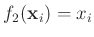 festgesetzt
werden. In diesem Fall ergibt sich daraus das Modell der linearen Regression
festgesetzt
werden. In diesem Fall ergibt sich daraus das Modell der linearen Regression
![$\displaystyle \bm{\mathrm{E}}[y_i] = \theta_1 + \theta_2 x_i \hspace{15mm} i = 1,\ldots,n$](img64.png) |
(6) |
mit den unbekannten Parametern 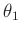 und
und 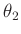 . In ähnlicher
Weise lassen sich auch das Modell für eine Gerade durch den
Koordinatenursprung oder für die Anpassung mit einem Polynom
herleiten.
. In ähnlicher
Weise lassen sich auch das Modell für eine Gerade durch den
Koordinatenursprung oder für die Anpassung mit einem Polynom
herleiten.
Durch die Wahl der 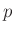 Funktionen
Funktionen
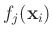 und der
und der 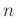 Messstellen
Messstellen 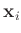 sind die Werte
sind die Werte
fest vorgeben. Diese 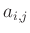 bilden die
bilden die
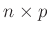 Design-Matrix
Design-Matrix
des linearen Modells, das damit als einfache Matrizengleichnung geschrieben
werden kann.
![$\displaystyle \bm{y} = \bm{A}\;\bm{\theta} + \bm{\epsilon} \hspace{5mm} \mathrm{beziehungsweise} \hspace {5mm} \bm{\mathrm{E}}[\bm{y}] = \bm{A}\;\bm{\theta}$](img75.png) |
(7) |
Bisher wurde vorausgesetzt, dass alle Messergebnisse die gleiche
Genauigkeit besitzen. Dies ist oftmals nicht der Fall und die
einzelnen Messwerte sollen daher mit unterschiedlicher Gewichtung in das
Modell einfließen. Zu diesem Zweck kann zu jedem Messwert ein entsprechendes
Gewicht 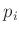 festgelegt werden. Damit lassen sich die relativen
Unterscheide in der Genauigkeit der einzelnen Messungen in einfacher
Weise beschreiben. Diese Werte bilden die Gewichtsmatrix
festgelegt werden. Damit lassen sich die relativen
Unterscheide in der Genauigkeit der einzelnen Messungen in einfacher
Weise beschreiben. Diese Werte bilden die Gewichtsmatrix
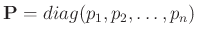 . Setzt man für
. Setzt man für
so ergibt
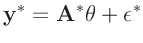 |
(9) |
wieder ein lineares Modell (Gleichung 7).
Liegen Informationen über die Varianz 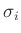 der Fehler der
einzelnen Messwerte
der Fehler der
einzelnen Messwerte 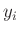 vor, so können diese zur Gewichtung
benutzt werden. Dazu geht man von der Vorstellung aus, dass die
einzelnen Messwerte
vor, so können diese zur Gewichtung
benutzt werden. Dazu geht man von der Vorstellung aus, dass die
einzelnen Messwerte 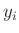 jeweils Mittelwerte einer Sichprobe des
Umfanges
jeweils Mittelwerte einer Sichprobe des
Umfanges 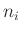 repräsentieren. Die Varianz dieser Mittelwerte folgt
aus der Varianz
repräsentieren. Die Varianz dieser Mittelwerte folgt
aus der Varianz 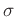 der zugrunde liegenden Grundgesamtheit
entsprechend
der zugrunde liegenden Grundgesamtheit
entsprechend
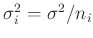 . Setzt man als Gewichte
den Umfang der jeweiligen Stichproben ein, wie dies auch
von Fahrmeir (2009) für gruppierte Daten beschrieben wird,
so folgt daraus:
. Setzt man als Gewichte
den Umfang der jeweiligen Stichproben ein, wie dies auch
von Fahrmeir (2009) für gruppierte Daten beschrieben wird,
so folgt daraus:
Da oftmals die Varianz 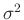 der Grundgesamtheit vorab nicht
bekannt ist, werden die Gewichte nur proportional zu
der Grundgesamtheit vorab nicht
bekannt ist, werden die Gewichte nur proportional zu 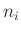 angesetzt.
angesetzt.
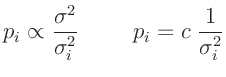 |
(10) |
wobei c in diesem Fall, eine willkürlich festgelegte Konstante3ist, die, wie später zu sehen sein wird, keinen Einfluss auf die
Schätzungen von
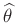 (Gleichung 12) und
(Gleichung 12) und
![$ \widehat{\bm{\mathrm{Cov}}[\widehat{\bm{\theta}}]}$](img101.png) (Gleichung 14)
hat.
(Gleichung 14)
hat.
Die Diagonalmatrix
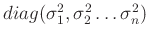 entspricht der
entspricht der 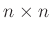 Kovarianzmatrix
Kovarianzmatrix
![$ \bm{\mathrm{Cov}}[\bm{\epsilon}]$](img104.png) der
bisher als statistisch unabhängig angenommenen Abweichungen
der
bisher als statistisch unabhängig angenommenen Abweichungen
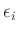 der Messwerte
der Messwerte 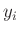 von den aus dem Modell berechneten
Werten. Diese Annahme ist im weiteren nicht mehr erforderlich. Die
Kovarianzmatrix der Messabweichungen
von den aus dem Modell berechneten
Werten. Diese Annahme ist im weiteren nicht mehr erforderlich. Die
Kovarianzmatrix der Messabweichungen
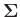 ist allgemein
gegeben durch:
ist allgemein
gegeben durch:
wobei
sind. Die Kovarianzmatrix
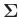 ist symmetrisch und positiv
semidefinit. Ist sie positiv definit, kann ihre Inverse, auch als
Präzisionsmatrix bezeichnet, zur Festlegung der Gewichtmatrix genutzt
werden.
ist symmetrisch und positiv
semidefinit. Ist sie positiv definit, kann ihre Inverse, auch als
Präzisionsmatrix bezeichnet, zur Festlegung der Gewichtmatrix genutzt
werden.
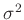 ist hierbei der Varianzfaktor, oftmals auch als Varianz der
Gewichtseinheit bezeichnet, der festlegt welchem Messwert das Gewicht
Eins gegeben wird. Bei unbekanntem
ist hierbei der Varianzfaktor, oftmals auch als Varianz der
Gewichtseinheit bezeichnet, der festlegt welchem Messwert das Gewicht
Eins gegeben wird. Bei unbekanntem 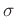 wird die Gewichtsmatrix als
proportional zur Präzisionsmatrix angesetzt.
wird die Gewichtsmatrix als
proportional zur Präzisionsmatrix angesetzt.
 |
(11) |
Für die Konstante 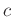 gilt das oben gesagte.
gilt das oben gesagte.
Setzt man für die Gewichtsmatrix die Einheitsmatrix ein,
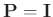 , so ergibt sich daraus das einfache lineare Modell
(Gleichung 7). Eine getrennte Behandlung dieses
Spezialfalles ist im weiteren nicht erforderlich.
, so ergibt sich daraus das einfache lineare Modell
(Gleichung 7). Eine getrennte Behandlung dieses
Spezialfalles ist im weiteren nicht erforderlich.
Unterabschnitte
schaefer
2017-12-09
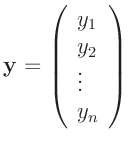
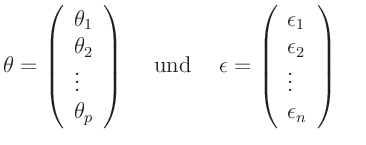
![$\displaystyle \bm{\mathrm{E}}[y_i] =\sum_{j=1}^p \theta_j f_j(\bm{x}_i) \hspace{15mm} i = 1,\ldots,n$](img59.png)
![]() Funktionen
Funktionen
![]() und der
und der ![]() Messstellen
Messstellen ![]() sind die Werte
sind die Werte

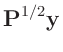
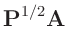
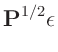
![]() der Fehler der
einzelnen Messwerte
der Fehler der
einzelnen Messwerte ![]() vor, so können diese zur Gewichtung
benutzt werden. Dazu geht man von der Vorstellung aus, dass die
einzelnen Messwerte
vor, so können diese zur Gewichtung
benutzt werden. Dazu geht man von der Vorstellung aus, dass die
einzelnen Messwerte ![]() jeweils Mittelwerte einer Sichprobe des
Umfanges
jeweils Mittelwerte einer Sichprobe des
Umfanges ![]() repräsentieren. Die Varianz dieser Mittelwerte folgt
aus der Varianz
repräsentieren. Die Varianz dieser Mittelwerte folgt
aus der Varianz ![]() der zugrunde liegenden Grundgesamtheit
entsprechend
der zugrunde liegenden Grundgesamtheit
entsprechend
![]() . Setzt man als Gewichte
den Umfang der jeweiligen Stichproben ein, wie dies auch
von Fahrmeir (2009) für gruppierte Daten beschrieben wird,
so folgt daraus:
. Setzt man als Gewichte
den Umfang der jeweiligen Stichproben ein, wie dies auch
von Fahrmeir (2009) für gruppierte Daten beschrieben wird,
so folgt daraus:
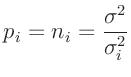
![$ \widehat{\bm{\mathrm{Cov}}[\widehat{\bm{\theta}}]}$](img101.png) (Gleichung 14)
hat.
(Gleichung 14)
hat.
![]() entspricht der
entspricht der ![]() Kovarianzmatrix
Kovarianzmatrix
![]() der
bisher als statistisch unabhängig angenommenen Abweichungen
der
bisher als statistisch unabhängig angenommenen Abweichungen
![]() der Messwerte
der Messwerte ![]() von den aus dem Modell berechneten
Werten. Diese Annahme ist im weiteren nicht mehr erforderlich. Die
Kovarianzmatrix der Messabweichungen
von den aus dem Modell berechneten
Werten. Diese Annahme ist im weiteren nicht mehr erforderlich. Die
Kovarianzmatrix der Messabweichungen
![]() ist allgemein
gegeben durch:
ist allgemein
gegeben durch:
![$\displaystyle \bm{\Sigma} = \bm{\mathrm{Cov}}[\bm{\epsilon}]=\left( \begin{arra...
...
\sigma_{n,1} & \sigma_{n,2} & \cdots & \sigma_{n,n}\\
\end{array} \right)
$](img108.png)
![]() , so ergibt sich daraus das einfache lineare Modell
(Gleichung 7). Eine getrennte Behandlung dieses
Spezialfalles ist im weiteren nicht erforderlich.
, so ergibt sich daraus das einfache lineare Modell
(Gleichung 7). Eine getrennte Behandlung dieses
Spezialfalles ist im weiteren nicht erforderlich.