Auswertung Versuch O8 mit GnuPlot
Mit Hilfe der Fraunhoferschen Näherung kann das Kirchhoffsche
Beugungsintegral auf einfache Weise gelöst werden. Dazu werden zwei
Annahmen gemacht:
- Das auf das beugende Objekt fallende Licht ist parallelen und kann
daher mit ebenen Wellenfronten beschrieben werden.
- Die Beugungserscheinungen an diesem Objekt, dessen beugende
Strukturen sich innerhalb eines Kreises mit dem Radius
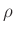 befinden, werden im Fernfeld betrachtet. Dies bedeutet, dass der
Beobachtungsabstand
befinden, werden im Fernfeld betrachtet. Dies bedeutet, dass der
Beobachtungsabstand 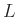 zum beugenden Objekt groß ist, dass die
Fresnelzahl
zum beugenden Objekt groß ist, dass die
Fresnelzahl
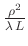 sehr viel kleiner als 1 ist.
sehr viel kleiner als 1 ist.
Im weiteren wird auch davon ausgegangen, dass die beugenden Blenden
und der Schirm zur Beobachtung der Beugungsbilder senkrecht zur
Ausbreitungsrichtung der einfallenden Lichtwellen angeordnet sind.
Unter diesen Voraussetzungen können die für die Beugung relevanten
Abmessungen, wie die Breite eines Spalts oder der Durchmesser einer
Lochblende, auf einfache Weise aus den beobachteten Beugungsbilder
bestimmt werden. Die Messunsicherheit, die dabei erreicht werden kann,
ist deutlich kleiner als die, die mit anderen direkten optischen
Messmethoden, zum Beispiel der Bestimmung mit Hilfe eines
Lichtmikroskops möglich ist.
Die Intensität des an einem Einzelspalt gebeugten Lichts wird
unter den oben genannten Annahmen durch die Proportionalität
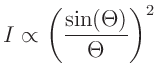 mit mit 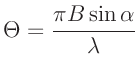 |
(1) |
bestimmt (Lipson, Lipson, Tannhauser, Optik (1997), Seite 175). Hierbei bezeichnet 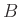 die
Breite des Spalts,
die
Breite des Spalts, 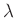 die Wellenlänge des Lichts und
die Wellenlänge des Lichts und 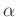 den Winkel zur
Ausbreitungsrichtung der einfallenden ebenen Lichtwellen. Die Minima
dieser Funktion liegen bei
den Winkel zur
Ausbreitungsrichtung der einfallenden ebenen Lichtwellen. Die Minima
dieser Funktion liegen bei
Mit Hilfe der doppelten Kleinwinkelnäherung,
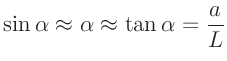 |
(2) |
ergibt zwischen der Ordnung 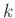 und dem Abstand
und dem Abstand 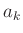 der
Minima vom zentralen Hauptmaximum ein linearer Zusammenhang
der
Minima vom zentralen Hauptmaximum ein linearer Zusammenhang
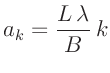 |
(3) |
Aus dem Anstieg dieser Geraden und den bekannten Größen 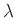 und
und
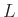 kann die Spaltbreite berechnet werden. Diese Vorgehensweise ist
immer dann zulässig, wenn der relative Fehler der Kleinwinkelnäherung
deutlich kleiner ist als die relative Messunsicherheit des Abstandes
kann die Spaltbreite berechnet werden. Diese Vorgehensweise ist
immer dann zulässig, wenn der relative Fehler der Kleinwinkelnäherung
deutlich kleiner ist als die relative Messunsicherheit des Abstandes
Diese Bedingung ist erfüllt, wenn für die Messunsicherheit von 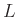 gilt:
gilt:
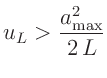 |
(4) |
wobei
 der größte beobachtete Minimaabstand ist.
der größte beobachtete Minimaabstand ist.
Auf Grund der hohen Intensität und der Breite des Hauptmaximums ist
dessen genaue Lage auf dem Beobachtungsschirm nur sehr schwer zu
bestimmen. Unter Ausnutzung der Symmetrie des Beugungsbilds kann
dieses Problem umgangen werden. Werden die Positionen der Minima
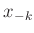 und
und 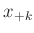 auf beiden Seiten des Hauptmaximums auf einer
willkürlich positionierten Längenskala bestimmt, so gilt:
auf beiden Seiten des Hauptmaximums auf einer
willkürlich positionierten Längenskala bestimmt, so gilt:
Die Lage des Hauptmaximums ist für alle Werte von 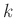 durch
durch
bestimmt. Eine Betrachtung mit dem Fehlerfortpflanzungsgesetz ergibt,
dass die Unsicherheiten der so bestimmten Werte von 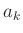 und
und
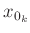 identisch sind. Das bedeutet, das die Standardabweichung des
Mittelwertes
identisch sind. Das bedeutet, das die Standardabweichung des
Mittelwertes
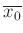 mit der Standardabweichung der einzelnen
mit der Standardabweichung der einzelnen 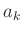 Werte übereinstimmt und
daher als Maß für deren Messunsicherheit benutzt werden kann.
Bei dieser Art der Auswertung muss die Gerade (Gleichung
3) zwingend durch den Nullpunkt gehen. Es kann
keinen physikalisch oder messtechnisch begründeten Offset geben.
Werte übereinstimmt und
daher als Maß für deren Messunsicherheit benutzt werden kann.
Bei dieser Art der Auswertung muss die Gerade (Gleichung
3) zwingend durch den Nullpunkt gehen. Es kann
keinen physikalisch oder messtechnisch begründeten Offset geben.
Da bei dieser Messreihe nur sehr wenige Daten mit
GnuPlot
ausgewertet werden, kann die Tabelle mit den Werten für
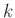 ,
, 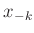 und
und 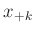 als inline Daten direkt in
die Datei mit den GnuPlot-Befehlen aufgenommen werden.
als inline Daten direkt in
die Datei mit den GnuPlot-Befehlen aufgenommen werden.
#k xlinks xrechts
$data « EOD
10 47 143
9 53 138
8 57 134
7 63 129
6 67 125
5 72 120
4 77 116
3 82 111
2 87 106
1 92 101
EOD
Die Standardabweichung der Mittelpunktslage kann neben vielen weiteren
statistischen Parametern aus diesen Werten direkt berechnet werden.
stats $data using (($2+$3)/2)
n = STATS_records
mw = STATS_mean
std = STATS_ssd
Die im weiteren noch benötigten Werte, die Anzahl der Datenpunkte,
der Mittelwert der Lage des Hauptmaximums 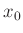 sowie dessen
Standardabweichung, werden dabei gleich in entsprechend benannten
Variablen gespeichert. Nach der Definition der sehr einfachen
Fitfunktion und dem sinnvollen Setzen des Anfangswertes für den
einzigen Parameter
sowie dessen
Standardabweichung, werden dabei gleich in entsprechend benannten
Variablen gespeichert. Nach der Definition der sehr einfachen
Fitfunktion und dem sinnvollen Setzen des Anfangswertes für den
einzigen Parameter 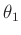 kann die Fitroutine aufgerufen werden.
kann die Fitroutine aufgerufen werden.
a(x) = theta1*x
theta1=5
fit a(x) $data using 1:(($3-$2)/2) via theta1
Dieser Fit erfolgte ohne Gewichtung, da bei dieser Auswertemethode die
Messunsicherheiten aller Abstände 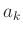 gleich der Standardabweichung
von
gleich der Standardabweichung
von 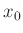 sind. Die Berücksichtigung des systematischen Restfehlers
der zur Messung der Minimalagen verwendeten Längenskala ergibt nur
sehr geringe Unterschiede zwischen den einzelnen Messunsicherheiten
sind. Die Berücksichtigung des systematischen Restfehlers
der zur Messung der Minimalagen verwendeten Längenskala ergibt nur
sehr geringe Unterschiede zwischen den einzelnen Messunsicherheiten
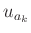 , so dass auch in diesem Fall auf eine Gewichtung verzichtet
werden kann.
, so dass auch in diesem Fall auf eine Gewichtung verzichtet
werden kann.
Nach dem Setzen sinnvoller Werte für die Beschriftung und den
Plotbereich kann die Grafik mit den Messdaten und der berechneten
Ausgleichsgeraden gezeichnet werden. Der Wert der Standardabweichung
von 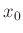 wird zur Darstellung der Fehlerintervalle genutzt.
wird zur Darstellung der Fehlerintervalle genutzt.
set xlabel "Ordnung"
set xrange [0:n+1]
set ylabel "a [mm]"
plot $data using 1:(($3-$2)/2):(std) with errorbars pt 7 ps 0.75\
title "measured data", a(x) title "linear fit"
Abbildung 1:
Beugung am Spalt: gemessene Abstände der Minima vom
Hauptmaximum und daraus berechnete Ausgleichsgerade
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-1a}
\end{picture}
\end{center}\end{figure}](Timg44.png) |
Aus dem Wert des Fitparameters 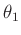 und dessen Fehler, beide Werte
werden im Terminalfenster von GnuPlot angezeigt und können der
Datei fit.log entnommen werden, kann bei bekanntem Abstand
und dessen Fehler, beide Werte
werden im Terminalfenster von GnuPlot angezeigt und können der
Datei fit.log entnommen werden, kann bei bekanntem Abstand 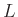 und
bekannter Wellenlänge
und
bekannter Wellenlänge 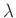 die Breite des beugenden Spalts
die Breite des beugenden Spalts
und durch Anwendung des Fehlerfortpflanzungsgesetzes die zugehörige
Unsicherheit berechnet werden.
Für die Lagen der Minima des Beugungsbilds des Spalts auf einer
willkürlich positionierten Skala ergibt sich unter Anwendung der
Kleinwinkelnäherung (Gleichung 2) der Zusammenhang:
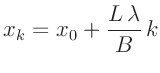 |
(5) |
Hierbei bedeutet 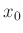 die Lage des Hauptmaximums. Bei dieser Art der
Auswertung gibt es keine statistisch begründete Möglichkeit, die
Messunsicherheit der einzelnen
die Lage des Hauptmaximums. Bei dieser Art der
Auswertung gibt es keine statistisch begründete Möglichkeit, die
Messunsicherheit der einzelnen 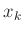 Werte zu bestimmen, so dass diese
nur unter Berücksichtigung des systematische Restfehlers der verwendeten
Skala und der konkreten Messbedingungen abgeschätzt werden kann.
Auch in diesem Fall kann auf eine Gewichtung verzichtet werden, da
sich die ergebenden Messunsicherheiten
Werte zu bestimmen, so dass diese
nur unter Berücksichtigung des systematische Restfehlers der verwendeten
Skala und der konkreten Messbedingungen abgeschätzt werden kann.
Auch in diesem Fall kann auf eine Gewichtung verzichtet werden, da
sich die ergebenden Messunsicherheiten 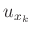 nur wenig
unterscheiden werden.
nur wenig
unterscheiden werden.
Der für der Auswertung notwendige Datensatz enthält nur die zwei
Spalten für k und 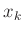
$data « EOD
-10 47
-9 53
-8 57
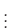
8 134
9 138
10 143
EOD
Wenn eine Gewichtung nicht notwendig ist, können für den Fall eines
einfachen Geradenausgleiches
die Parameter 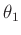 und
und 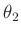 und deren Fehler mit dem Befehls
und deren Fehler mit dem Befehls
stats $data
berechnet und im Terminalfenster ausgegeben werden. Um diese Werte
auch in weiteren Rechnungen zu benutzen sollten sie in geeignet
benannte Variablen übernommen werden.
theta1=STATS_intercept
utheta1=STATS_intercept_err
theta2=STATS_slope
utheta2=STATS_slope_err
Für die Darstellung der erhaltene Ausgleichsgerade, der Messdaten und deren
abgeschätzten Messunsicherheiten, sind noch einige weitere Größen zu definieren.
uy=0.5
y(x) = theta1+theta2*x
set xlabel "Ordnung"
set ylabel "Minima Position [mm]"
Danach kann die Graphik erstellt werden.
plot $data using 1:2:(uy) with errorbars pt 7 ps 0.75 \
title "measured data", y(x) title "linear fit"
Abbildung 2:
Beugung am Spalt: gemessene Lagen der Minima und daraus
berechnete Ausgleichsgerade
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-1b}
\end{picture}
\end{center}\end{figure}](Timg58.png) |
Wie im vorigen Abschnitt kann bei bekanntem Abstand 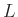 und bekannter
Wellenlänge
und bekannter
Wellenlänge 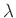 aus dem Wert des Anstiegs
aus dem Wert des Anstiegs 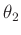 die Spaltbreite
die Spaltbreite
berechnet werden. Mit Hilfe des Fehlerfortpflanzungsgesetzes ergibt
sich aus den Unsicherheiten 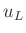 ,
, 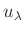 und
und
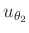 die Unsicherheit
der Spaltbreite.
die Unsicherheit
der Spaltbreite.
Die Intensitätsverteilung des an einer Lochblende gebeugten Lichts
lässt sich in der Fraunhoferschen Näherung mit der Gleichung
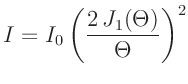 mit mit 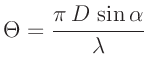 |
(6) |
beschreiben (Lipson, Lipson, Tannhauser, Optik (1997), Seite 178). 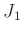 bezeichnet hierbei
die Besselfunktion 1.Ordnung.
bezeichnet hierbei
die Besselfunktion 1.Ordnung. 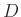 ist der Durchmesser der Lochblende,
ist der Durchmesser der Lochblende, 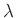 die
Wellenlänge des verwendeten Lichts und
die
Wellenlänge des verwendeten Lichts und 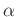 den Beobachtungswinkel
bezogen auf die optischen Achse.
den Beobachtungswinkel
bezogen auf die optischen Achse.
Eine erste Abschätzung des Durchmessers der beugenden Lochblende kann
mit Hilfe des Winkels des ersten Minimas 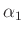 vorgenommen
werden, für das gilt:
vorgenommen
werden, für das gilt:
Wenn die Bedingung der Gleichung 4 erfüllt ist,
kann auch hier wieder die Kleinwinkelnäherung
angewendet werden. Der Wert 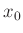 bezeichnet die Lage des
0.Maximums auf der Messskala
bezeichnet die Lage des
0.Maximums auf der Messskala 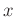 .
. 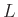 ist der Abstand zwischen der
Lochblende und dem Eintrittsspalt der verwendeten Photodiode. Damit
ergibt sich für
ist der Abstand zwischen der
Lochblende und dem Eintrittsspalt der verwendeten Photodiode. Damit
ergibt sich für 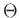 der vereinfachte Ausdruck:
der vereinfachte Ausdruck:
Die Größen 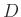 ,
, 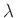 und
und 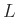 können zu einem Geometrieparameter
zusammengefasst werden, in den zur Vereinfachung der nächsten Schritte
auch noch die Konstante
können zu einem Geometrieparameter
zusammengefasst werden, in den zur Vereinfachung der nächsten Schritte
auch noch die Konstante 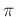 aufgenommen wird.
aufgenommen wird.
Mit dem sich ergebenden Ausdruck für 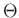
kann die Fitfunktion für die gemessenen Intensitätsverteilung 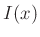 aufgestellt werden,
aufgestellt werden,
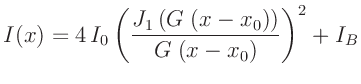 |
(7) |
die als anzupassende Parameter die Größen 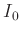 ,
, 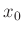 , und
, und 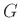 enthält.
enthält. 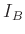 wurde als zusätzliche, von
wurde als zusätzliche, von 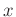 unabhängige Größe
eingeführt, um das nicht zu vermeidende Restlicht zu berücksichtigen.
Dieser ,,Dunkelstrom`` kann einfach durch Unterbrechung des
Strahlenganges vor der Lochblende gemessen werden und liegt meistens
mehr als eine Größenordnung unter dem kleinsten in der
Intensitätsverteilung gemessenen Strom.
unabhängige Größe
eingeführt, um das nicht zu vermeidende Restlicht zu berücksichtigen.
Dieser ,,Dunkelstrom`` kann einfach durch Unterbrechung des
Strahlenganges vor der Lochblende gemessen werden und liegt meistens
mehr als eine Größenordnung unter dem kleinsten in der
Intensitätsverteilung gemessenen Strom.
Um die Daten mit
GnuPlot
auszuwerten, ist als erstes die Erstellung einer Datei mit den
Messdaten in tabellarischer Form erforderlich. Die erste Spalte
enthält die gemessene x-Position (z.B. in mm), die zweite den
gemessenen Strom (z.B. in nA). Als Beispiel soll im weiteren die Datei
Messdaten-20170317-Platz4.txt
verwendet werden. Das Einlesen und Darstellen der Daten aus der
vorbereiteten Datei erfolgt durch Eingabe des Befehls:
set logscale y
plot "Messdaten-20170317-Platz4.txt" using 1:2
Dabei wird eine logarithmische y-Skala verwendet, damit auch die
Nebenmaxima dargestellt werden.
Die Definition der Intensitätsverteilung hinter der Lochblende
erfolgt durch:
I(x) = (x==x0) ? I0+Ib : \
I0*(2*besj1(G*(x-x0))/(G*(x-x0)))**2+Ib
Die Stelle 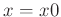 erfordert eine besondere Behandlung, da an dieser
Stelle eine Division durch 0 auftritt, die einen Abbruch der
Fitroutine zur Folge hätte. Der Grenzwert
erfordert eine besondere Behandlung, da an dieser
Stelle eine Division durch 0 auftritt, die einen Abbruch der
Fitroutine zur Folge hätte. Der Grenzwert
ist eindeutig definiert. Als nächstes werden die notwendigen numerischen Größen, die
aus dem ersten Plot abgeschätzt werden können, festgelegt.
D=0.3
lambda=632.8*10**-6
l=1591
G=pi*D/(lambda*l)
x0=6.5
I0=7300
Ib=0.007
Alle Längen sind hier in 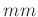 und alle Ströme in
und alle Ströme in 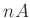 angegeben. Dies
kann gleich in die Beschriftung der Achsen aufgenommen werden.
angegeben. Dies
kann gleich in die Beschriftung der Achsen aufgenommen werden.
set xlabel "x [mm]"
set ylabel "I [nA]"
Damit kann I(x) zusammen mit den Messdaten angezeigt werden.
set logscale
plot "Messdaten-20170317-Platz4.txt" using 1:2, I(x)
Durch manuelle Veränderung des unbekannten Wertes für den
Blendendurchmesser kann man versuchen, die Anpassung an die Messdaten
manuell weiter zu verbessern und einen guten Startwerte für den
nichtlinearen Fitalgorithmus zu finden. Danach kann der erste
ungewichtete Fit erfolgen.
fit I(x) "Messdaten-20170317-Platz4.txt" using 1:2 via x0,I0,G
Da es sich bei 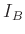 , im Unterschied zu
, im Unterschied zu 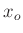 und
und 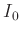 , um eine
direkt gemessene, von
, um eine
direkt gemessene, von 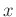 unabhängige Größe handelt, sollte dieser
Wert nicht als Fitparameter verwendet werden. Das Ergebnis kann mit
unabhängige Größe handelt, sollte dieser
Wert nicht als Fitparameter verwendet werden. Das Ergebnis kann mit
set logscale y
set samples 2500
plot "Messdaten-20170317-Platz4.txt" using 1:2 \
title "measured data", I(x) title "fitted curve I(x)"
dargestellt werden. Zur richtigen Darstellung der Minima wurde die
Zahl der Stützstellen für die Berechnung der Fitfunktion gegenüber dem
Standardwert 100 deutlich erhöht. Dafür sind in diesem Fall 2500
Stützstellen notwendig.
Abbildung 3:
Beugung an einer Lochblende: gemessene
Intensitätsverteilung
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-2a}
\end{picture}
\end{center}\end{figure}](Timg102.png) |
In dieser Darstellung fällt auf, dass die
Abweichungen zwischen den Messdaten und der Fitkurve im Bereich der
Minima besonders ausgeprägt sind. Ursache dafür ist die Breite des
Eintrittsspaltes vor der Photodiode, die größer als Null sein
muss. Dies führt dazu, dass der gemessene Strom dem Integral über einen
durch die Breite diese Eintrittsspaltes bestimmten Bereich der
theoretischen Intensitätsverteilung entspricht.
Um die gemessenen Intensitätsverteilung richtig zu beschreiben, ist die
Auswirkung der Auflösungsfunktion 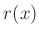 des Eintrittsspaltes zu
berücksichtigen. Die Auflösungsfunktion
des Eintrittsspaltes zu
berücksichtigen. Die Auflösungsfunktion 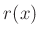 kann durch eine
Rechteckfunktion
kann durch eine
Rechteckfunktion 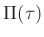 beschrieben werden.
beschrieben werden.
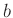 ist dabei die halbe Breite des Eintrittsspaltes. Für
diese Auflösungsfunktion gilt mit
ist dabei die halbe Breite des Eintrittsspaltes. Für
diese Auflösungsfunktion gilt mit 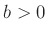
Die gemessene Intensität 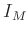 ergibt sich aus der Faltung
der durch Gleichung 7 gegebenen Intensitätsverteilung
ergibt sich aus der Faltung
der durch Gleichung 7 gegebenen Intensitätsverteilung 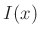 mit der Auflösungsfunktion
mit der Auflösungsfunktion 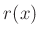 des Eintrittsspaltes.
des Eintrittsspaltes.
Dieses Faltungsintegral kann analytisch gelöst werden. Unter
Ausnutzung der Distributivität der Faltung
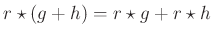 und der Assoziativität mit der skalaren Multiplikation
und der Assoziativität mit der skalaren Multiplikation
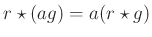 sowie durch Ersetzen des Terms
sowie durch Ersetzen des Terms 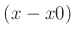 durch
durch 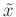 lässt sich obige
Gleichung einfach umformen (siehe hierzu : Mathematica Notebook
O8-LoesungFaltungsintegral.nb
und
O8-ConvolutionSpaltPhotodiode.nb).
Man erhält für den gemessenen Strom :
lässt sich obige
Gleichung einfach umformen (siehe hierzu : Mathematica Notebook
O8-LoesungFaltungsintegral.nb
und
O8-ConvolutionSpaltPhotodiode.nb).
Man erhält für den gemessenen Strom :
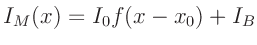 |
(8) |
mit
Für
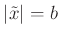 kann der Wert von
kann der Wert von
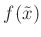 nicht
numerisch berechnet werden. Der Grenzwert
nicht
numerisch berechnet werden. Der Grenzwert
ist definiert und kann anstelle von
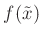 genutzt werden.
Der Wert von
genutzt werden.
Der Wert von
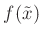 an der Stelle
an der Stelle
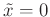
ist sowohl von 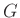 als auch von
als auch von 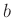 abhängig. Dies führt zu einer
unnötigen, beim Fitten störenden Korrelation zwischen
abhängig. Dies führt zu einer
unnötigen, beim Fitten störenden Korrelation zwischen 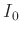 und
und 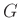 sowie zwischen
sowie zwischen 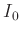 und
und 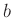 . Um dies zu vermeiden, sollte anstelle
von Gleichung 8 der Ausdruck
. Um dies zu vermeiden, sollte anstelle
von Gleichung 8 der Ausdruck
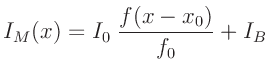 |
(9) |
verwendet werden.
Diese Funktion wird in
GnuPlot
am besten aus mehrere Teilfunktionen zusammengesetzt. Zuerst werden die
drei Hilfsfunktionen f0(b,G), fb(b,G) und f(x)
f0(b,G) = (2*b**2*G**2-1)*(besj1(b*G))**2/(b*G**2) \
+ 2*b*(besj0(b*G))**2-2*besj0(b*G)*besj1(b*G)/G
fb(b,G) = (2*b**2*G**2-0.25)*(besj1(2*b*G))**2/(b*G**2) \
+ 2*b*(besj0(2*b*G))**2-besj0(2*b*G)*besj1(2*b*G)/G
f(x) = (abs(x)==b)? fb(b,G) : \
(G**2*(b-x)**2-0.5)*(besj1(G*(b-x)))**2/(G**2*(b-x)) \
+ (G**2*(b+x)**2-0.5)*(besj1(G*(b+x)))**2/(G**2*(b+x)) \
+ (b-x)*(besj0(G*(b-x)))**2 \
+ (b+x)*(besj0(G*(b+x)))**2 \
- (besj0(G*(b-x)))*(besj1(G*(b-x)))/G \
- (besj0(G*(b+x)))*(besj1(G*(b+x)))/G
definiert, mit deren Hilfe dann die eigentliche Fitfunktion festgelegt wird.
I(x) = (x==x0)? I0+Ib : I0*f(x-x0)/f0(b,G)+Ib
Die weiteren Schritte sind analog der oben beschriebenen
Vorgehensweise. Die dort erhaltenen Ergebnisse können als Startwerte
verwendet werden. Für die Breite des Eintrittsspaltes wird ein Wert
von etwa einem Millimeter angenommen.
b = 0.5
Ib=0.007
fit I(x) "Messdaten-20170317-Platz4.txt" using 1:2 via x0,I0,G,b
Zur richtigen Darstellung der Minima beim Zeichnen ist die Zahl der
Stützstellen wieder deutlich zu erhöhen.
set samples 2500
set logscale y
plot "Messdaten-20170317-Platz4.txt" using 1:2 \
title "measured data", I(x) title "fitted curve I(x)"
Die graphische Darstellung zeigt, dass die Anpassung an die Daten
deutlich besser ist.
Abbildung 4:
Messdaten und berechnete Fitfunktion unter
Berücksichtigung der Breite des Eintrittsspaltes
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-2b}
\end{picture}
\end{center}\end{figure}](Timg142.png) |
Dennoch weicht die berechnete Fitfunktion im Bereich der Minima immer
noch deutlich von den Messwerten ab. Diese Differenzen werden bei
höheren Ordnungen noch auffälliger und betreffen fast alle Punkte
mit kleinen Werten des gemessenen Stromes.
Der durchgeführten
Ausgleichsrechnung lag die Annahme zu Grunde, dass alle Stromwerte mit
der gleichen Messunsicherheit bestimmt wurden. Daher wurde auf eine
Gewichtung verzichtet. Im Anbetracht der Tatsache, dass der
Wertebereich der Strommessung fünf Größenordnungen umfasst, ist diese
Annahme nicht gerechtfertigt und es muss eine Gewichtung durchgeführt
werden.
Die Intensität des an der Lochblende gebeugten Lichtes wird mit einer
als Stromquelle betriebenen Silizium-Photodiode gemessen, die im
Quasi-Kurzschluss betrieben wird. In dieser Betriebsart ist der Strom in
Sperrrichtung über viele Größenordnungen linear von der
Bestrahlungsstärke abhängig. Es gilt:
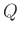 ist die Ladungsmenge, die innerhalb der Zeitspanne
ist die Ladungsmenge, die innerhalb der Zeitspanne 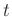 durch die
auftreffenden Photonen in der Photodiode generiert wird. Der Wert des
Quantenwirkungsgrades der Photodiode
durch die
auftreffenden Photonen in der Photodiode generiert wird. Der Wert des
Quantenwirkungsgrades der Photodiode 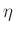 , die Elementarladung
, die Elementarladung 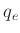 und die interne Zeitkonstante
und die interne Zeitkonstante 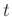 des verwendeten Picoamperemeters
werden im weiteren zu der Konstanten
des verwendeten Picoamperemeters
werden im weiteren zu der Konstanten 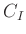 zusammengefasst. Damit kann
man für I schreiben:
zusammengefasst. Damit kann
man für I schreiben:
Die Anzahl der Photonen ist poissonverteilt. Damit gilt für die
Standardabweichung des gemessenen Stromes
wobei der Wert der Größe
 nicht bekannt ist. Für die
Festlegung von Gewichtsfaktoren, ist es nicht notwendig den genauen
Wert der einzelnen Messunsicherheiten zu kennen, die gegebene Proportionalität ist
ausreichend. Da es sich bei der hier diskutierten Gewichtung zwar um eine
physikalisch begründete Abschätzung der Messunsicherheit handelt, die darin
enthaltene Proportionalitätskonstante
nicht bekannt ist. Für die
Festlegung von Gewichtsfaktoren, ist es nicht notwendig den genauen
Wert der einzelnen Messunsicherheiten zu kennen, die gegebene Proportionalität ist
ausreichend. Da es sich bei der hier diskutierten Gewichtung zwar um eine
physikalisch begründete Abschätzung der Messunsicherheit handelt, die darin
enthaltene Proportionalitätskonstante
 jedoch unbekannt ist,
muss die Option errorscaling gesetzt sein. Dies entspricht der
Grundeinstellung von GnuPlot.
jedoch unbekannt ist,
muss die Option errorscaling gesetzt sein. Dies entspricht der
Grundeinstellung von GnuPlot.
set fit errorscaling
Nun ist noch die Funktion zur Berechnung von 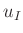 zu
definieren. Dabei wird für die Proportionalitätskonstante der
Einfachheit halber der Wert 1 festgelegt. Damit ergibt sich:
zu
definieren. Dabei wird für die Proportionalitätskonstante der
Einfachheit halber der Wert 1 festgelegt. Damit ergibt sich:
u(I)=sqrt(I)
Die Ergebnisse des ungewichteten Fits können als sinnvolle
Startwerte benutzt werden.
x0=6.45069
I0=7249.12
G=0.845147
b=0.628305
Ib=0.007
Danach kann der Fit mit den vier Parametern x0, I0, G
und b gestartet und das Ergebnis zusammen mit den Messdaten
dargestellt werden. Die zur Gewichtung benötigten Messunsicherheiten
werden dabei aus den Messwerten berechnet.
fit I(x) "Messdaten-20170317-Platz4.txt" \
using 1:2:(u($2)) yerr via x0,I0,G,b
set logscale y
set samples 2500
plot "Messdaten-20170317-Platz4.txt" using 1:2 \
title "measured data", I(x) title "fitted curve I(x)"
Ein Plotten der Fehlerintervalle der Messdaten ist auf Grund der
Tatsache, dass nur die Proportionalität zu den aus der
Poisson-Verteilung abgeschätzten Unsicherheiten genutzt wurde, nicht
sinnvoll.
Abbildung 5:
Messdaten und berechnete Fitfunktion unter
Berücksichtigung der Breite des Eintrittsspaltes mit Gewichtung
nach Poisson-Verteilung
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-2c}
\end{picture}
\end{center}\end{figure}](Timg161.png) |
Allein schon der Vergleich mit dem ungewichteten Fit (Abbildung
4) zeigt, dass sich die Anpassung der Fitkurve
an die Messdaten noch einmal deutlich verbessert hat. Ein Vergleich
der Werte
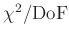 (DoF steht für die Anzahl der
Freiheitsgrade) ist hier nicht möglich, da einmal ohne und einmal mit
Gewichtung gefitted wurde. Im ersten Fall entspricht der Wert
(DoF steht für die Anzahl der
Freiheitsgrade) ist hier nicht möglich, da einmal ohne und einmal mit
Gewichtung gefitted wurde. Im ersten Fall entspricht der Wert
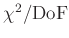 der Restvarianz, dem Teil der Gesamtvarianz, der
nicht durch den Fit erklärt wird. Im zweiten Fall gibt der Wert
der Restvarianz, dem Teil der Gesamtvarianz, der
nicht durch den Fit erklärt wird. Im zweiten Fall gibt der Wert
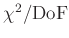 die Varianz der Gewichtseinheit an, die von dem
bei der Gewichtung frei gewählten Proportionalitätsfaktor abhängt.
die Varianz der Gewichtseinheit an, die von dem
bei der Gewichtung frei gewählten Proportionalitätsfaktor abhängt.
Wenn Angaben zum systematischen Restfehler des verwendeten
Strommessgerätes bekannt sind, können diese zur Gewichtung benutzt
werden. Das hier verwendete Picoamperemeter MV40 verfügt über
insgesamt 16 Messbereiche (300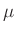 A, 100
A, 100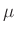 A, 30
A, 30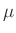 A, 10
A, 10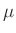 A,
3
A,
3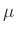 A, 1
A, 1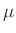 A, 300nA, 100nA, 30nA, 10nA, 3nA, 1nA, 300pA, 100pA,
30pA, 10pA), die sich über mehr als 7 Größenordnungen erstrecken. Der
Hersteller gibt den Gerätefehler mit 1,5% des Messbereichsendwertes
an. In den Picoampere-Bereichen kommt noch eine Unsicherheit von 3pA
hinzu. Geht man davon aus, das immer im jeweils kleinst möglichen
Messbereich gemessen wurde, lässt sich die Unsicherheit
A, 300nA, 100nA, 30nA, 10nA, 3nA, 1nA, 300pA, 100pA,
30pA, 10pA), die sich über mehr als 7 Größenordnungen erstrecken. Der
Hersteller gibt den Gerätefehler mit 1,5% des Messbereichsendwertes
an. In den Picoampere-Bereichen kommt noch eine Unsicherheit von 3pA
hinzu. Geht man davon aus, das immer im jeweils kleinst möglichen
Messbereich gemessen wurde, lässt sich die Unsicherheit 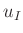 der
Strommessung aus dem jeweiligen Messwert ableiten.
der
Strommessung aus dem jeweiligen Messwert ableiten.
GK = 0.015
ZF = 0.003
u(I) = (I>100000)? GK*300000 : (I>30000)? GK*100000 :\
(I>10000)? GK*30000 : (I>3000)? GK*10000 : (I>1000)? GK*3000 :\
(I>300)? GK*1000 : (I>100)? GK*300 : (I>30)? GK*100 :\
(I>10)? GK*30 : (I>3)? GK*10 : (I>1)? GK*3 : (I>0.3)? GK*1.0:\
(I>0.1)? GK*0.3+ZF : (I>0.03)? GK*0.1+ZF :\
(I>0.01)? GK*0.03+ZF : GK*0.01+ZF
Die Ergebnisse des ungewichteten Fits können auch in diesem Fall als
sinnvolle Startwerte genutzt werden. Zum Starten der Fitroutine wird
der gleiche GnuPlot Befehl genutzt wie im Fall der Gewichtung
mittels Poisson-Verteilung.
x0=6.45069
I0=7249.12
G=0.845147
b=0.628305
Ib=0.007
fit I(x) "Messdaten-20170317-Platz4.txt" \
using 1:2:(u($2)) yerr via x0,I0,G,b
Das Ergebnis dieses Fits hängt sehr empfindlich von der Wahl der
Startwerte für die Fitparameter ab. Schon kleine Änderungen können
dazu führen, dass das angewendete Marquardt-Levenberg-Verfahren in
einem lokalen und nicht im globalen Minimum konvergiert. In der
graphischen Darstellung wird dies meist sofort deutlich. Hier helfen
oftmals nur das Wissen über die physikalischen Zusammenhänge und über
die genutzten statistischen Verfahren sowie Erfahrung und Inspiration
weiter. Nicht um sonst heißt es im GnuPlot-Manual unter Verweis auf
das fudgit Projekt: ``Nonlinear fitting is an art!''.
Da in diesem Fall abgeschätzte Messunsicherheiten genutzt wurden,
können in der graphischen Darstellung diese als Fehlerbalken mit
eingezeichnet werden.
set logscale y
set samples 2500
plot "Messdaten-20170317-Platz4.txt" using 1:2:(u($2)) \
with errorbars pt 7 ps 0.5 title "measured data", \
I(x) title "fitted curve I(x)"
Abbildung 6:
Messdaten und berechnete Fitfunktion unter
Berücksichtigung der Breite des Eintrittsspaltes mit
instrumenteller Gewichtung
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-2d}
\end{picture}
\end{center}\end{figure}](Timg172.png) |
Auf Grund der verwendeten unterschiedlichen Methoden zur Berechnung
der Gewichte, einmal auf Grundlage der erwarteten statistischen
Verteilung, einmal auf Grundlage der Herstellerangaben zur
Messunsicherheit des verwendeten Messgeräts, ist ein Vergleich der
beiden
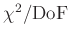 Werte nicht zulässig.
Werte nicht zulässig.
Ähnlich wie bei der Auswertung der Beugung am Spalt kann aus dem
letztendlich erhaltenen Wert des Parameters 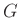 bei bekanntem Abstand
bei bekanntem Abstand
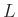 und bekannter Wellenlänge
und bekannter Wellenlänge 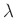 der gesuchte
Blendendurchmesser
der gesuchte
Blendendurchmesser 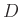 und dessen Unsicherheit berechnet werden.
und dessen Unsicherheit berechnet werden.
Als letztes ist noch GnuPlot zu beenden:
quit
-
Lipson, Stephen G., Lipson, Henry S., and Tannhauser, David S.
Optik, Mit 125 Aufgaben und vollständigen Lösungen. Optical Physics <dt.>
Springer-Lehrbuch. Berlin [u.a.]: Springer, 1997
-
http://www.springer.com/de/book/9783540619123
abgerufen am 11.4.2017 12:06 Uhr
schaefer
2019-04-03
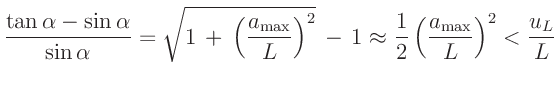
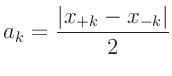
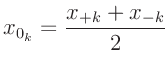
![]() ,
, ![]() und
und ![]() als inline Daten direkt in
die Datei mit den GnuPlot-Befehlen aufgenommen werden.
als inline Daten direkt in
die Datei mit den GnuPlot-Befehlen aufgenommen werden.
![]() sowie dessen
Standardabweichung, werden dabei gleich in entsprechend benannten
Variablen gespeichert. Nach der Definition der sehr einfachen
Fitfunktion und dem sinnvollen Setzen des Anfangswertes für den
einzigen Parameter
sowie dessen
Standardabweichung, werden dabei gleich in entsprechend benannten
Variablen gespeichert. Nach der Definition der sehr einfachen
Fitfunktion und dem sinnvollen Setzen des Anfangswertes für den
einzigen Parameter ![]() kann die Fitroutine aufgerufen werden.
kann die Fitroutine aufgerufen werden.
![]() gleich der Standardabweichung
von
gleich der Standardabweichung
von ![]() sind. Die Berücksichtigung des systematischen Restfehlers
der zur Messung der Minimalagen verwendeten Längenskala ergibt nur
sehr geringe Unterschiede zwischen den einzelnen Messunsicherheiten
sind. Die Berücksichtigung des systematischen Restfehlers
der zur Messung der Minimalagen verwendeten Längenskala ergibt nur
sehr geringe Unterschiede zwischen den einzelnen Messunsicherheiten
![]() , so dass auch in diesem Fall auf eine Gewichtung verzichtet
werden kann.
, so dass auch in diesem Fall auf eine Gewichtung verzichtet
werden kann.
![]() wird zur Darstellung der Fehlerintervalle genutzt.
wird zur Darstellung der Fehlerintervalle genutzt.
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-1a}
\end{picture}
\end{center}\end{figure}](Timg44.png)
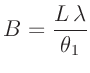
![]()
![]()
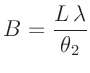
![]() vorgenommen
werden, für das gilt:
vorgenommen
werden, für das gilt:
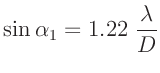
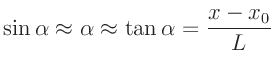
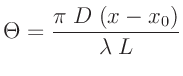
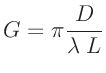
![]() erfordert eine besondere Behandlung, da an dieser
Stelle eine Division durch 0 auftritt, die einen Abbruch der
Fitroutine zur Folge hätte. Der Grenzwert
erfordert eine besondere Behandlung, da an dieser
Stelle eine Division durch 0 auftritt, die einen Abbruch der
Fitroutine zur Folge hätte. Der Grenzwert
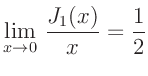
![]() des Eintrittsspaltes zu
berücksichtigen. Die Auflösungsfunktion
des Eintrittsspaltes zu
berücksichtigen. Die Auflösungsfunktion ![]() kann durch eine
Rechteckfunktion
kann durch eine
Rechteckfunktion ![]() beschrieben werden.
beschrieben werden.
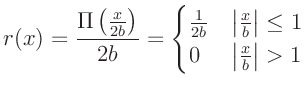
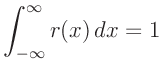
![]() ergibt sich aus der Faltung
der durch Gleichung 7 gegebenen Intensitätsverteilung
ergibt sich aus der Faltung
der durch Gleichung 7 gegebenen Intensitätsverteilung ![]() mit der Auflösungsfunktion
mit der Auflösungsfunktion ![]() des Eintrittsspaltes.
des Eintrittsspaltes.
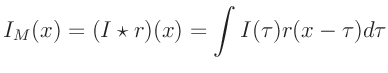
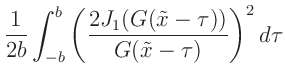
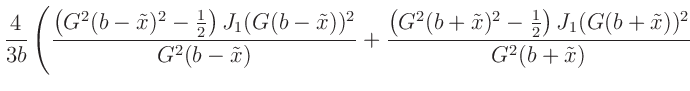
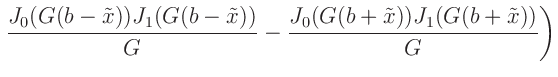
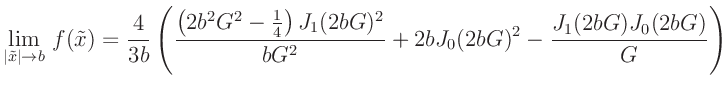
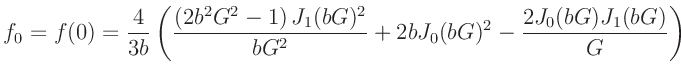
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-2b}
\end{picture}
\end{center}\end{figure}](Timg142.png)
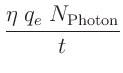
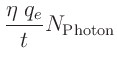
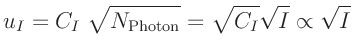
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-2c}
\end{picture}
\end{center}\end{figure}](Timg161.png)
![]() (DoF steht für die Anzahl der
Freiheitsgrade) ist hier nicht möglich, da einmal ohne und einmal mit
Gewichtung gefitted wurde. Im ersten Fall entspricht der Wert
(DoF steht für die Anzahl der
Freiheitsgrade) ist hier nicht möglich, da einmal ohne und einmal mit
Gewichtung gefitted wurde. Im ersten Fall entspricht der Wert
![]() der Restvarianz, dem Teil der Gesamtvarianz, der
nicht durch den Fit erklärt wird. Im zweiten Fall gibt der Wert
der Restvarianz, dem Teil der Gesamtvarianz, der
nicht durch den Fit erklärt wird. Im zweiten Fall gibt der Wert
![]() die Varianz der Gewichtseinheit an, die von dem
bei der Gewichtung frei gewählten Proportionalitätsfaktor abhängt.
die Varianz der Gewichtseinheit an, die von dem
bei der Gewichtung frei gewählten Proportionalitätsfaktor abhängt.
![]() A, 100
A, 100![]() A, 30
A, 30![]() A, 10
A, 10![]() A,
3
A,
3![]() A, 1
A, 1![]() A, 300nA, 100nA, 30nA, 10nA, 3nA, 1nA, 300pA, 100pA,
30pA, 10pA), die sich über mehr als 7 Größenordnungen erstrecken. Der
Hersteller gibt den Gerätefehler mit 1,5% des Messbereichsendwertes
an. In den Picoampere-Bereichen kommt noch eine Unsicherheit von 3pA
hinzu. Geht man davon aus, das immer im jeweils kleinst möglichen
Messbereich gemessen wurde, lässt sich die Unsicherheit
A, 300nA, 100nA, 30nA, 10nA, 3nA, 1nA, 300pA, 100pA,
30pA, 10pA), die sich über mehr als 7 Größenordnungen erstrecken. Der
Hersteller gibt den Gerätefehler mit 1,5% des Messbereichsendwertes
an. In den Picoampere-Bereichen kommt noch eine Unsicherheit von 3pA
hinzu. Geht man davon aus, das immer im jeweils kleinst möglichen
Messbereich gemessen wurde, lässt sich die Unsicherheit ![]() der
Strommessung aus dem jeweiligen Messwert ableiten.
der
Strommessung aus dem jeweiligen Messwert ableiten.
![\begin{figure}\begin{center}
\begin{picture}(120,90)
\includegraphics[width=120mm]{gnuplot-graphik-2d}
\end{picture}
\end{center}\end{figure}](Timg172.png)
![]() Werte nicht zulässig.
Werte nicht zulässig.
![]() bei bekanntem Abstand
bei bekanntem Abstand
![]() und bekannter Wellenlänge
und bekannter Wellenlänge ![]() der gesuchte
Blendendurchmesser
der gesuchte
Blendendurchmesser ![]() und dessen Unsicherheit berechnet werden.
und dessen Unsicherheit berechnet werden.