Klassische Statistik

Gesucht sind die Schätzwerte für $\widehat{\bm{\theta}}$ , $\widehat{\sigma^2}$ und $\widehat{\bm{\mathrm{Cov}}[\widehat{\bm{\theta}}]}$ , die den wahren Werten der unbekannten Parameter möglichst nahe kommen. Bei der Methode der kleinsten Quadrate bestimmt das Minimum der Summe der quadrierten Abweichung

$$Q(\bm{\theta}) = \sum_{i=1}^n\sum_{j=1}^n (y_i -\bm{\mathrm{E}}[y_i])p_{i,j} (y_j -\bm{\mathrm{E}}[y_j])$$

$$= \bm{\epsilon}^T\bm{P}\bm{\epsilon}$$

$$= (\bm{y} - \bm{A}\;\bm{\theta})^T\bm{P}(\bm{y}-\bm{A}\;\bm{\theta})$$

$$= \bm{y}^T\bm{P}\bm{y}-2\bm{\theta}^T\bm{A}^T\bm{P}\bm{y}+\bm{\theta}^T\bm{A}^T\bm{P}\bm{A}\;\bm{\theta}$$

die Schätzwerte der Parameter. Aus

$$\frac{\partial\,Q(\bm{\theta})}{\partial\,\bm{\theta}} = - 2 \bm{A}^T\bm{P}\bm{y} + 2 \bm{A}^T\bm{P}\bm{A}\;\bm{\theta} = \bm{0}$$

folgt unmittelbar:

$$\widehat{\bm{\theta}} = (\bm{A}^T\bm{P}\bm{A})^{-1}\,\bm{A}^T\bm{P}\bm{y}$$ (12)

Der Schätzwert für die Varianz der Messabweichungen kann aus dem Minimum von $Q(\bm{\theta})$ bestimmt werden.

$$\widehat{\sigma^2} = \frac{1}{n-p}\,Q(\bm{\theta})_{min} = \frac{... ...y}-\bm{A}\;\widehat{\bm{\theta}})^T\bm{P}(\bm{y}-\bm{A}\;\widehat{\bm{\theta}})$$ (13)

Für die Kovarianzmatrix von $\widehat{\bm{\theta}}$ ergibt sich damit:⁴

$$\widehat{\bm{\mathrm{Cov}}[\widehat{\bm{\theta}}]} = \widehat{\sigma^2}(\bm{A}^T\bm{P} \bm{A})^{-1}$$ (14)

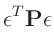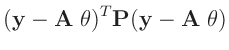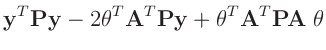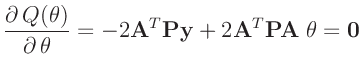
Bisher wurden keine Annahmen über die Verteilung der Messdaten zu Grunde gelegt. Die optimalen Eigenschaften der Methode der kleinsten Quadrate folgen einzig aus der Linearität des Modells. Wird für die Messabweichungen $\bm{\epsilon}$ eine Normalverteilung angenommen, führt die Maximum-Likelihood-Schätzung von $\widehat{\bm{\theta}}$ beziehungsweise die Restringierte Maximum-Likelihood-Schätzung ⁵von $\widehat{\sigma^2}$ zu dem gleichen Ergebnis. Unter dieser Voraussetzung sind sind auch die geschätzten Werte $\widehat{\bm{\theta}} \sim \mathrm{N}(\bm{\theta},\sigma^2(\bm{A}^T\bm{P}\bm{A})^{-1})$ normalverteilt.

Das Konfidenzintervall (Fehlerintervall) eines geschätzten Parameters $\widehat{\theta_j}$ wird durch die Wahrscheinlichkeit $P$ bestimmt, mit der dieser im Intervall $d_ {min} < \theta_j < d_{max}$ liegt

$$P(d_ {min} < \theta_j < d_{max}) = 1 - \alpha$$

wobei $1 - \alpha$ das Signifikanzniveau⁶angibt. Zur Festlegung der Intervallgrenzen $d$ wird der Test der Hypothese $H_0\mathrm{:}\;\theta_j = d$ verwendet. Dieser basiert auf der Teststatistik

$$t = \frac{\widehat{\theta_j} - d}{s_j}$$

mit

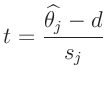
$$s_j = \widehat{\bm{\mathrm{Var}}[\widehat{\theta_j}]}^{1/2} = \l... .../2} = \left(\widehat{\sigma^2}(\bm{A}^T\bm{P} \bm{A})^{-1}_{j,j}\right)^{1/2}$$

Die Hypothese $H_0$ wird abgelehnt, wenn sich

$$\vert t\vert > t_{n-p}(1-\alpha/2)$$

ergibt. Hierbei bedeutet $t_{n-p}(1-\alpha/2)$ das $(1-\alpha/2)$-Quantil der Standard t-Verteilung⁷mit $n-p$ Freiheitsgraden . Die Grenzen des Konfidenzintervalls zum Signifikanzniveau $(1-\alpha)$ werden somit bestimmt durch

$$d_{min,max} = \widehat{\theta_j} \mp t_{n-p}(1-\alpha/2)\; s_j$$ (15)

Ähnliche Gleichungen kann man in vielen Lehrbüchern zur klassischen Statistik, z.B in Nollau (1975) (152ff), James (2006) (183ff), Fahrmeir (2009) (124ff), Martin (2012) (145ff) oder Wakefield (2013) (214ff) finden, wobei teilweise anstelle der Gewichtsmatrix $\bm{P}$ direkt die inverse Kovarianzmatrix $\bm{\Sigma}^{-1}$ benutzt oder das erste Element des Parametervektors $\bm{\theta}$ mit $\theta_0$ bezeichnet wird.