Im Einführungsskript findet man auf Seite 42 die Aussage:
,, Die Standardabweichungen für die beiden Parameter ... erhält man
durch Anwendung des Fortpflanzungsgesetzes für die
Unsicherheiten``. Als Quelle kann hier das im Vorwort erwähnte
Buch Bevington (2003) vermutet werden. Dort findet sich auf
Seite 109 die Herleitung der im Einführungsskript verwendeten
Formeln. Eine ähnliche Aussage wie im Einführungsskript ist auch
bei Wolff (2014) auf Seite 118 zu finden, ohne dass dazu eine
Begründung oder eine Quellenangabe erfolgt.
Was bedeutet die Anwendung der Fehlerfortpflanzung auf das Allgemeine
Lineare Modell? Dazu wird zuerst eine skalare Größe 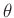 betrachtet,
die eine beliebige Funktion des
betrachtet,
die eine beliebige Funktion des 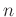 dimensionalen Vektors
dimensionalen Vektors 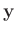 ist.
ist.
Wenn die Fehler
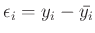 mit
mit
![$ \bar{y_i} = \bm{\mathrm{E}}[y_i]$](img400.png) klein sind, kann
die Taylorentwicklung von
klein sind, kann
die Taylorentwicklung von
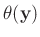 in der Umgebung des
Punktes
in der Umgebung des
Punktes
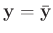 nach der ersten Ordnung
abgebrochen werden.
nach der ersten Ordnung
abgebrochen werden.
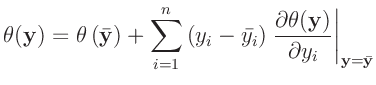 |
(24) |
Für die Varianz von
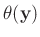 gilt:
gilt:
Wird die Taylorentwicklung 24 in diese Gleichung eingesetzt,
ergibt sich:
Dabei sind die
die Elemente der Kovarianzmatrix
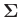 des Vektors
des Vektors 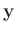 .
Wird außerdem
.
Wird außerdem
gesetzt, erhalten wir das allgemeine Fehlerfortpflanzungsgesetz
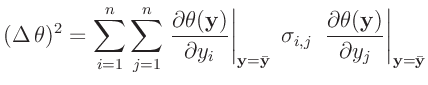 |
(25) |
Für den Fall, dass die Werte des Vektors 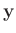 nicht korreliert
sind, wenn für
nicht korreliert
sind, wenn für 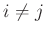 gilt
gilt
![$ \bm{\mathrm{Cov}}[y_i,y_j] = 0$](img418.png) ,
vereinfacht sich die Gleichung 25 zu der häufig verwendeten Form:
,
vereinfacht sich die Gleichung 25 zu der häufig verwendeten Form:
mit
![$ (\Delta\,y_i)^2 = \sigma_{i,i} = \bm{\mathrm{Var}}[y_i]$](img420.png) .
.
Das allgemeine Fehlerfortpflanzungsgesetz 25 für eine Größe
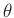 lässt sich auf den
lässt sich auf den 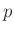 -dimensionalen Vektor
-dimensionalen Vektor
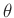 erweitern. Dessen Elemente
erweitern. Dessen Elemente 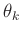 sind alle
Funktionen des selben Vektors
sind alle
Funktionen des selben Vektors 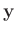 und daher korreliert. Für die
Elemente der Kovarianzmatrix
und daher korreliert. Für die
Elemente der Kovarianzmatrix
![$ \bm{\mathrm{Cov}}[\bm{\theta}]$](img426.png) gilt dann:
gilt dann:
![$\displaystyle \bm{\mathrm{Cov}}[\theta_k,\theta_l] = \sum_{i=1}^n\sum_{j=1}^n \...
...; \left.\frac{\partial\theta_l}{\partial y_j}\right\vert _{\bm{y}=\bar{\bm{y}}}$](img427.png) |
(26) |
Wird eine
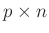 Matrix
Matrix 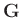 mit den Elementen
mit den Elementen
eingeführt, kann Gleichung 26 als Matrizengleichung geschrieben
werden.
![$\displaystyle \bm{\mathrm{Cov}}[\bm{\theta}] = \bm{G} \, \bm{\Sigma} \, \bm{G}^T$](img431.png) |
(27) |
Bezeichnet man die
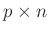 Matrix
Matrix
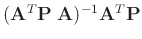 aus Gleichung 12
mit
aus Gleichung 12
mit  , dann kann die Gleichung 12 auch geschrieben
werden als:
, dann kann die Gleichung 12 auch geschrieben
werden als:
Aus dieser Darstellung wird sofort klar, dass für die einzelne
Elemente der Matrix  gilt:
gilt:
Damit kann aus den Gleichungen 27 und
11 die Beziehung
abgeleitet 17werden. Die so bestimmte Kovarianzmatrix enthält die, bei der
Aufstellung des Allgemeinen Linearen Modells willkürlich festlegbare
Konstante 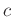 . Alle aus der Kovarianzmatrix abgeleiteten
Fehlerintervalle sind daher von der Festlegung dieser Konstanten
abhängig. Nur wenn die Kovarianzmatrix
. Alle aus der Kovarianzmatrix abgeleiteten
Fehlerintervalle sind daher von der Festlegung dieser Konstanten
abhängig. Nur wenn die Kovarianzmatrix
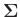 vollständig bekannt ist, oder
aus den vorliegenden Daten bestimmt werden kann, so wie es von
Grabe (2011) im Kapitel 21 beschrieben wird, führt die Festlegung
vollständig bekannt ist, oder
aus den vorliegenden Daten bestimmt werden kann, so wie es von
Grabe (2011) im Kapitel 21 beschrieben wird, führt die Festlegung
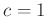 beziehungsweise
beziehungsweise
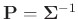 zu richtigen
Ergebnissen. Nur in diesem Fall gilt:
zu richtigen
Ergebnissen. Nur in diesem Fall gilt:
![$\displaystyle \bm{\mathrm{Cov}}[\bm{\theta}] = (\bm{A}^T\bm{\Sigma}^{-1}\bm{A})^{-1}$](img466.png) |
(29) |
Auf diesen Umstand macht auch Bevington (2003) auf Seite 108
aufmerksam. Er schlägt vor, die bestimmten Varianzen, die Quadrate der
Fehlerintervalle, zu korrigieren, sie mit dem Wert von
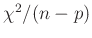 zu multiplizieren, wenn
zu multiplizieren, wenn
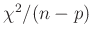 zu stark von 1
abweicht. Genau dann ergibt sich die von von der klassischen Statistik
(Gleichung 14) berechnet Kovarianzmatrix. Auf
die zwingende Notwendigkeit der Berücksichtigung des Varianzfaktors
zu stark von 1
abweicht. Genau dann ergibt sich die von von der klassischen Statistik
(Gleichung 14) berechnet Kovarianzmatrix. Auf
die zwingende Notwendigkeit der Berücksichtigung des Varianzfaktors
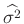 weist auch Martin (2012) ausdrücklich im
Abschnitt 8.1.2 hin. Wird dies unterlassen, dann führt die Anwendung
des Fehlerfortpflanzungsgesetzes auf das Allgemeine Lineare Modell zu
falschen Ergebnissen.
weist auch Martin (2012) ausdrücklich im
Abschnitt 8.1.2 hin. Wird dies unterlassen, dann führt die Anwendung
des Fehlerfortpflanzungsgesetzes auf das Allgemeine Lineare Modell zu
falschen Ergebnissen.
Damit ist die Ursache der Widersprüche in Tabelle 2
geklärt. Die Formeln aus dem Einführungsskript (2007) liefern das
gleiche falsche Ergebnis wie die Mathematica Routine
,,LinearModelFit`` mit der Option
,,VarianceEstimatorFunction
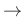 (1&)``. In beiden
Fällen wird der Varianzfaktor auf den Wert 1 festgelegt. Ob das auch
bei QtiPlot der Fall ist, wird im weiteren noch untersucht.
(1&)``. In beiden
Fällen wird der Varianzfaktor auf den Wert 1 festgelegt. Ob das auch
bei QtiPlot der Fall ist, wird im weiteren noch untersucht.
Da in der im Einführungsskript (2007) auf Seite 42 angegebenen
Gleichung 45 der Varianzfaktor nicht berücksichtigt wird und dort
auch die obigen Hinweise in keiner Weise erwähnt werden, ist diese
Gleichung und die ihr zu Grunde liegende Vorgehensweise als falsch zu
betrachten.
schaefer
2017-12-09
![]() betrachtet,
die eine beliebige Funktion des
betrachtet,
die eine beliebige Funktion des ![]() dimensionalen Vektors
dimensionalen Vektors ![]() ist.
ist.
![$\displaystyle \bm{\mathrm{Var}}[\theta(\bm{y})]=\bm{\mathrm{E}}\left[\Big(\thet...
...eq \bm{\mathrm{E}}\left[\Big(\theta(\bm{y})-\theta(\bar{\bm{y}})\Big)^2\right]
$](img405.png)
![$\displaystyle \bm{\mathrm{E}}\left[\left( \sum_{i=1}^n\left(y_i-\bar{y_i}\right...
...heta(\bm{y})}{\partial y_i} \right\vert _{\bm{y}=\bar{\bm{y}}} \right)^2\right]$](img408.png)
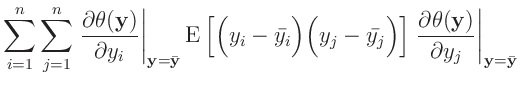
![$\displaystyle \bm{\mathrm{E}}\left[\Big(y_i-\bar{y_i}\Big)\Big(y_j-\bar{y_j}\Big)\right]
= \sigma_{i,j} = \bm{\mathrm{Cov}}[y_i,y_j]
$](img411.png)
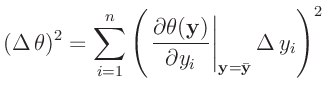
![]() lässt sich auf den
lässt sich auf den ![]() -dimensionalen Vektor
-dimensionalen Vektor
![]() erweitern. Dessen Elemente
erweitern. Dessen Elemente ![]() sind alle
Funktionen des selben Vektors
sind alle
Funktionen des selben Vektors ![]() und daher korreliert. Für die
Elemente der Kovarianzmatrix
und daher korreliert. Für die
Elemente der Kovarianzmatrix
![]() gilt dann:
gilt dann:
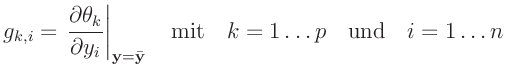
![]() Matrix
Matrix
![]() aus Gleichung 12
mit
aus Gleichung 12
mit ![]() , dann kann die Gleichung 12 auch geschrieben
werden als:
, dann kann die Gleichung 12 auch geschrieben
werden als:
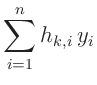
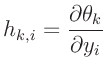
![]() (1&)``. In beiden
Fällen wird der Varianzfaktor auf den Wert 1 festgelegt. Ob das auch
bei QtiPlot der Fall ist, wird im weiteren noch untersucht.
(1&)``. In beiden
Fällen wird der Varianzfaktor auf den Wert 1 festgelegt. Ob das auch
bei QtiPlot der Fall ist, wird im weiteren noch untersucht.